Аксонометрическая проекция — Википедия

Материал из Википедии — свободной энциклопедии

Проецирование параллелепипеда на плоскость П’.

Аксонометри́ческая прое́кция (от др.-греч. ἄξων «ось» + μετρέω «измеряю») — способ изображения геометрических предметов на чертеже при помощи параллельных проекций.

Предмет с системой координат, к которой он отнесён, проецируют на произвольную плоскость (картинная плоскость аксонометрической проекции) таким образом, чтобы эта плоскость не совпадала с его координатной плоскостью. В этом случае получаются две взаимосвязанные проекции одной фигуры на одну плоскость, что позволяет восстановить положение в пространстве, получив наглядное изображение предмета. Так как картинная плоскость не параллельна ни одной из координатных осей, то имеются искажения отрезков по длине параллельных координатным осям. Это искажение может быть равным по всем трём осям — изометрическая проекция, одинаковыми по двум осям — диметрическая проекция и с искажениями разными по всем трём осям — триметрическая проекция.

Стандартизированные аксонометрические проекции ^[1][править | править код]

Аксонометрическая проекция

• прямоугольная проекция (направление проецирования перпендикулярно к плоскости проекции):
• косоугольная проекция (направление проецирования не перпендикулярно к плоскости проекции):
  • фронтальная изометрическая проекция;
  • фронтальная диметрическая проекция;
  • горизонтальная изометрическая проекция.

Проекция (геометрия)

1. ↑ По ГОСТ 2.317-69 — Единая система конструкторской документации. Аксонометрические проекции.

1. Богданов В. Н., Малежик И. Ф., Верхола А. П. и др. Справочное руководство по черчению. — М.: Машиностроение, 1989. — С. 864. — ISBN 5-217-00403-7.
2. Под ред. Ишлинский А. Ю. Новый политехнический словарь. — М.: Большая Российская энциклопедия, 2003. — С. 671. — ISBN 5-7107-7316-6.
3. Фролов С. А. Начертательная геометрия. — 2-е изд., перераб. и доп. — М.: Машиностроение, 1983. — С. 240.

Урок черчения «Получение и построение аксонометрических проекций»

УРОК № 9 Дата проведения:

Тема: «Получение и построение аксонометрических проекций ».

Тип урока: урок изучения нового материала.

Цели и задачи урока:

— познакомить с новым термином «аксонометрия»;

— сформировать понятие о косоугольной фронтальной диметрической и прямоугольной изометрической проекциях, их особенностях и различиях, расположении осей, принципах построения аксонометрических проекций;

— учить проецированию куба на фронтальную димметрическую и изометрическую проекцию, способам построения аксонометрических проекций плоских фигур;

— развивать пространственные представления и пространственное мышление;

— развитие навыков работы чертёжными инструментами;

— воспитывать аккуратность в графических построениях;

— воспитание целеустремлённость;

Оборудование: чертежные инструменты, тетрадь, учебник, таблица с изображением аксонометрии, объёмные детали.

 

Ход урока:

I. Организация учащихся на уроке.

Приветствие, проверка явки учащихся, проверка готовности к уроку, заполнение журнала.

II. Сообщение темы, целей урока.

III. Работа по теме урока:

1)Повторение и закрепление материала по проецированию на 3 плоскости проекций. Индивидуальные карточки – задания.

Построение третьего вида по двум данным.

Карточки вклеиваются в тетрадь и выполняются построения в карточке.

Дополнение чертёжа недостающими линиями.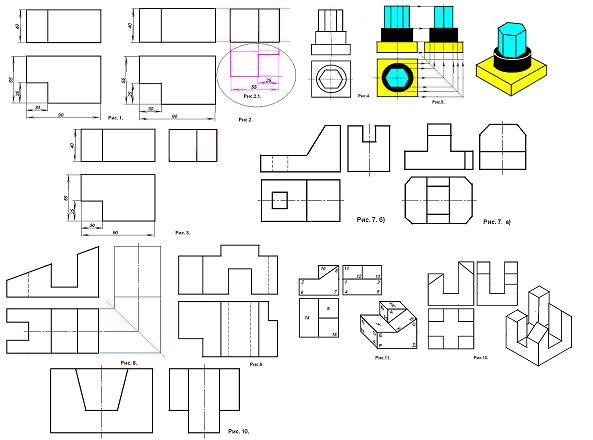

2) Аксонометрические проекции. (Изучение новых понятий с записью их в тетрадь).

Чертеж механизма или детали не дает полное представление о его форме. Поэтому чертежи сложных изделий сопровождают наглядными изображениями (аксонометрическими проекциями).

Аксонометрия — слово греческое, в переводе означает измерение по осям.

Проекции называются аксонометрическими потому, что предмет проецируется на плоскость вместе с осями координат.

При построении аксонометрических проекций размеры откладывают вдоль осей X,Y,Z — аксонометрические оси.

Аксонометрические проекции отличаются наглядностью. На аксонометрических проекциях форма предмета всегда передаётся одним изображением, позволяющим увидеть 3 его стороны.

Стандарт устанавливает несколько типов аксонометрических проекций. Мы познакомимся с 2 из них: косоугольной фронтальной диметрической и прямоугольной изометрической проекциями.

Фронтальная диметрическая проекция (диметрия).

При выполнении диметрической проекции перед плоскостью проекций предмет располагается так, чтобы его передняя грань была параллельна плоскости проекций. На аксонометрической плоскости проекций получают изображение координатных осей и косоугольную фронтальную димметрическую проекцию предмета. Оси X и Z отобразились на плоскость перпендикулярно друг другу, а ось Y под углом 45 к положению оси X.

Работа в тетрадях.

На листе в клетку отступите 8 клеток сверху и слева. Ось Z – вертикально, ось X – горизонтально, ось Y – под углом 45, по углам клеточек. Особенность данного вида проецирования в том, что мы видим без искажения переднюю сторону детали, то есть вид спереди. Однако стороны, расположенные вдоль оси Y, будут уменьшены в 2 раза по сравнению с оригиналом. Отсюда название «диметрия» — двойное измерение.

Прямоугольная изометрическая проекция.

Изометрия – это одна из аксонометрических проекций.

Изометрия (греч.) — равное измерение.

При вычерчивании изометрической проекции (изометрии) размеры по всем трем осям откладывают натуральные. Углы между аксонометрическими осями в этой проекции равны 120.

Работа в тетрадях.

На листе в клетку отступите 8 клеток сверху и слева. Ось Z – вертикально, ось X , ось Y – под углом 30 , отсчитайте 5 клеток в сторону и 3 клетки вниз.

Общие правила в выполнении аксонометрических проекций как в диметрии, так и в изометрии:

1. Ось Z всегда вертикальна.

2. Все измерения производятся только по аксонометрическим осям или по прямым, параллельным им.

3. Горизонтальные размеры отмеряются по осям X и Y.

III. Практическое закрепление пройденного материала.

1. Выполнение в тетради построения некоторых плоских геометрических фигур в аксонометрии. Начнём с квадрата со стороной 3 см (построение в диметрии и изометрии).

 

Теперь выполним построение простой плоскогранной фигуры (см. учебник стр. 50) .

Построение можно начинать выполнять с основания фигуры, либо с передней грани( главного вида). Обратите внимание на то, как нужно наносить размеры в аксонометрии: выносные линии являются продолжением сторон, расстояние между которыми они указывают, а размерную линию проводят параллельно той стороне детали, размер которой она указывает.

IV. Теоретическое закрепление изученного материала.

С каким видом проецирования мы сегодня познакомились?

Какие виды аксонометрических проекций узнали?

Чем они различаются?

Под каким углом оси располагаются в диметрии?

А в изометрии?

Какая ось всегда вертикальна?

Как по клеткам отложить угол 30 ?

V. Подведение итогов урока. Выставление оценок.

Домашнее задание:

§ 6,7, вопросы с. 42.

Аксонометрический чертеж — Большая Энциклопедия Нефти и Газа, статья, страница 1

Аксонометрический чертеж

Cтраница 1

Аксонометрический чертеж, или проекция, состоит всегда из одного изображения. Из рассмотрения аксонометрических; чертежей ( рис. За, б) нетрудно заметить, что, хотя на них форма и размеры деталей искажены, однако прочитать их значительно проще, чем комплексные, или, как принято говорить, аксонометрические чертежи обладают большей наглядностью.  [1]

Аксонометрический чертеж получается при параллельном проецировании оригинала на одну плоскость П2 вместе с некоторой координатной системой. Поскольку аксонометрический чертеж — однопроекционный, здесь уже безразлично, где находится плоскость проекций: ЗА или ПЕРЕД оригиналом.  [2]

Аксонометрический чертеж состоит только из одной параллельной проекции данного объекта, дополненной проекцией пространственной системы координат, к которой предварительно отнесен изображаемый объект.  [3]

Аксонометрические чертежи применяют в различных областях промышленности и при их зрительном воприятии наибольшую роль также играет информационный аспект. Алгоритмы построения аксонометрии позволяют изменять проецирующий аппарат. При неудачном выборе последнего вырождение инциденций может привести к неполноте аксонометрического чертежа и к потере возможности использовать этот чертеж как орудие исследования. Изложенное позволяет сделать вывод, что невырожденность инциденций оригинала на аксонометрическом чертеже является одним из критериев его оптимальности.  [4]

Аксонометрические чертежи обладают свойством наглядности и одновременно свойством обратимости — по таким чертежам легко представить общую форму предметов и их положение в пространстве.  [5]

Аксонометрический чертеж — это чертеж, состоящий из изображения на одной плоскости проекций предмета и координатных осей, к которым он отнесен вместе с натуральными масштабными отрезками по этим осям.  [6]

Аксонометрический чертеж детали, имеющий пустоты, следует выполнить с вырезами для выявления не только наружной, но и внутренней формы детали.  [7]

Только аксонометрический чертеж прямой, параллельной координатной плоскости IIj ( Oxy), имеет отличительную особенность: аксонометрическая и вторичная проекции прямой всегда параллельны. Сказанное справедливо и для чертежей прямых, параллельных координатным плоскостям II2 ( O.  [8]

Такой аксонометрический чертеж называют приведенным.  [9]

Рассмотрим аксонометрический чертеж прямой г, параллельной направлению проектирования.  [10]

Получим аксонометрический чертеж точки А.  [11]

Масштабы ортогонального и аксонометрического чертежа могут быть различными.  [12]

На аксонометрическом чертеже ( рис. 437 6) дуги круга преобразовались в дуги эллипса, также плавно сопрягающиеся в точках А, В, С, D, Е между собой и с прямыми линиями.  [13]

На аксонометрическом чертеже

могут быть нанесены размеры, обеспечивающие его обратимость. В этом случае отпадает необходимость в указании показателей искажения по осям.  [14]

На аксонометрических чертежах прямые, перпендикулярные и аксонометрической плоскости проекций ГГ ( на рис. 2.4 прямая т) и координатной плоскости IIj ( Oxy) ( на рис. 2.4 прямая п), называются проецирующими. Аксонометрическая и вторичная проекции прямых, перпендикулярных координатным плоскостям П2 ( СЬсг), П3 ( О.  [15]

Страницы:      1    2    3    4

Лекция 6 Аксонометрические проекции

Лекция 6. Аксонометрические проекции

Вопросы:

1.Общие сведения об аксонометрических проекциях.

2.Классификация аксонометрических проекций.

3.Примеры построения аксонометрических изображений .

1 Общие сведения об аксонометрических проекциях

При составлении технических чертежей иногда возникает необходимость наряду с изображениями предметов в системе ортогональных проекций иметь более наглядные изображения. Для таких изображений применяют метод аксонометрического проецирования (аксонометрия — греческое слово, в дословном переводе оно означает измерение по осям; аксон — ось, метрео — измеряю).

Сущность метода аксонометрического проецирования: предмет вместе с осями прямоугольных координат, к которым он отнесен в пространстве, проецируется на некоторую плоскость так, что ни одна из его координатных осей не проецируется на нее в точку, а значит сам предмет спроецируется на эту плоскость проекций в трех измерениях.

На черт. 88 на некоторую плоскость проекций Р спроецирована находящаяся в пространстве система координат х, y, z. Проекции хр, yр ,

zр осей координат на плоскость Р называются аксонометрическими осями.

Рисунок 88

На осях координат в пространстве отложены равные отрезки е. Как видно из чертежа, их проекции ех, еy, еz на плоскость Р в общем

случае не равны отрезку е и не равны между собой. Это значит, что размеры предмета в аксонометрических проекциях по всем трем осям искажаются. Изменение линейных размеров вдоль осей характеризуется показателями (коэффициентами) искажения вдоль осей.

Показателем искажения называется отношение длины отрезка на аксонометрической оси к длине такого же отрезка на соответствующей оси прямоугольной системы координат в пространстве.

Показателем искажения вдоль оси х обозначим буквой k, по оси y

– буквой m, по оси z – буквой n, тогда: k= ех/е; m= еy/е; n= еz/е.

Величина показателей искажения и соотношение между ними зависят от расположения плоскости проекций и от направления проецирования.

В практике построения аксонометрических проекций обычно пользуются не самими коэффициентами искажения, а некоторыми величинами, пропорциональными величинам коэффициентов искажения: К:М:N = k:m:n. Эти величины называют приведенными коэффициентами искажения.

2 Классификация аксонометрических проекций

Все множество аксонометрических проекций подразделяется на две группы:

1 Прямоугольные проекции – получены при направлении проецирования, перпендикулярном аксонометрической плоскости .

2 Косоугольные проекции – получены при направлении проецирования, выбранном под острым углом к аксонометрической плоскости.

Кроме того, каждая из указанных групп делится еще и по признаку соотношения аксонометрических масштабов или показател ей (коэффициентов) искажения. Пo этому признаку аксонометрические проекции можно разделить на следующие виды:

а) Изометрические — показатели искажения по всем трем осям одинаковы (изос — одинаковый).

б) Диметрические — показатели искажения по двум осям равны между собой, а третий не равен (ди — двойной).

в) Триметрические — показатели искажения по всем трем осям не рав-

ны между собой. Это аксонометрия (большого практического применения не имеет).

2.1 Прямоугольные аксонометрические проекции

Прямоугольная изометрическая проекция

Впрямоугольной изометрии все коэффициенты равны ме жду

собой:

k = m = n , k2 + m2 + n2=2 ,

тогда это равенство можно записать в виде 3k2=2, откуда k = .

Таким образом, в изометрии показатель искажения равен ~ 0,82. Это означает, что в прямоугольной

изометрии все размеры изображаемого предмета сокращаются в 0,82 раза. Для

упрощения	построений		используют
приведенные	коэффициенты		искажения
k=m=n=1,	что	соответствует
увеличению	размеров	изображения по
сравнению с действительными в 1,22
раза (1:0,82	1,22).	Расположение осей
изометрической проекции показано на рис.
89.			Рисунок 89

Прямоугольная диметрическая проекция

В прямоугольной диметрии показатели искажения по двум осям одинаковы, т. е. k = п. Третий

показатель искажения выбираем вдвое меньше двух других, т. е. m =1/2k. Тогда равенство k2+m2+n2= 2 примет такой вид: 2k2+1/4k2=2; откуда k=0,94;

	m = 0,47.
	В целях упрощения построений
	используем	приведенные
	коэффициенты искажения: k=n=1;
	m=0,5. Увеличение в этом случае
	составляет 6% (выражается числом		Рисунок 90
	1,06=1:0,94).	Расположение осей
	диметрической	проекции показано на
	рис. 90.

Рисунок 91

Рисунок 92

равны: k = n=1.

2.2 Косоугольные проекции

Фронтальная изометрическая проекция

На рис. 91 дано положение аксонометрических осей для фронтальной изометрии.

Согласно ГОСТ 2.317-69, допускается применять фронтальные изометрические проекции с углом наклона оси y 30° и 60°. Коэффициенты искажения являются точными и равны:

k = m = n=1.

Горизонтальная изометрическая проекция

На рис. 92 дано положение аксонометрических осей для фронтальной изометрии. Согласно ГОСТ 2.317-69, допускается применять горизонтальные изометрические проекции с углом наклона оси y 45° и 60° при сохранении угла между осями x и y 90°. Коэффициенты искажения являются точными и равны: к=m= n= 1.

Фронтальная диметрическая проекция

Положение осей такое же, как для фронтальной изометрии (рис.91) . Также допускается применение фронтальной диметрии с углом наклона оси y 30° и 60°.

Коэффициенты искажения являются точными и m=0.5

Все три вида стандартных косоугольных проекций получены при расположении одной из координатных плоскостей (горизонтальной или фронтальной) параллельно плоскости аксонометрии. Поэтому все фигуры, расположенные в этих плоскостях или им параллельных, проецируются на плоскость чертежа без искажения.

3 Примеры построения аксонометрических изображений

Как в прямоугольных (ортогональных проекциях), так и в аксонометрических одна проекция точки не определяет ее положения в пространстве. Помимо аксонометрической проекции точки необходимо иметь еще одну проекцию, называемую вторичной. Вторичная проекция точки – это аксонометрия одной из ее прямоугольных проекций (чаще горизонтальной).

Приемы построения аксонометрических изображений не зависят от вида аксонометрических проекций. Для всех проекций приемы построений одинаковы. Аксонометрическое изображение обычно строят на основе прямоугольных проекций предмета.

3.1 Аксонометрия точки

Построение аксонометрии точки по заданным ее ортогональным проекциям (рис. 93,а) начинаем с определения ее вторичной проекции (рис. 93,б). Для этого на аксонометрической оси х от начала координат откладываем величину координат Х точки А – ХA ; по оси y– отрезок YA (для диметрии YA×0.5 , т.к. показатель искажения по этой оси m=0.5).

В пересечении линий связи, проведенных параллельно осям из концов отмеренных отрезков, получают точку А1- вторичную проекцию точки А.

Аксонометрия точки А будет находиться на расстоянии Z A от вторичной проекции точки А.

Рисунок 93

3.2 Аксонометрия отрезка прямой (рис. 94)

Находим вторичные проекции точек А, В. Для этого откладываем вдоль осей х и у соответствующие координаты точек А и В. Затем отмечают на прямых, проведенных из вторичных проекций параллельно оси z, высоты точек А и В (Z A и ZB).Соединяем полученные точки – получаем аксонометрию отрезка.

Рисунок 94

3.3 Аксонометрия плоской фигуры

На рис. 95 показано построение изометрической проекции треугольника АВС. Находим вторичные проекции точек А, В, С. Для этого откладываем вдоль осей х и у соответствующие координаты точек А, В и С. Затем отмечаем на прямых, проведенных из вторичных проекций параллельно оси z, высоты точек А, В и С. Полученные точки соединяем линиями – получаем аксонометрию отрезка.

Рисунок 95

Если плоская фигура лежит в плоскости проекций, то аксонометрия такой фигуры совпадает с ее проекцией .

3.4 Аксонометрия окружностей, расположенных в плоскостях проекций

Окружности в аксонометрии изображаются в виде эллипсов. Для упрощения построений построение эллипсов заменяется построением овалов, очерченных дугами окружностей.

Прямоугольная изометрия окружности

	На рис. 96 в		прямоугольной
	изометрии изображен куб, в грани
	которого	вписаны		окружности.
	Грани	куба в	прямоугольной
	изометрии будут ромбами, а
	окружности – эллипсами. Длина
	большой оси эллипса равна 1.22d,
	где d — диаметр окружности. Малая
	ось составляет 0.7 d.
	На	рис.	97	показано
	построение овала, лежащего в
	плоскости, параллельной π1. Из
	точки пересечения осей О проводят
	вспомогательную			окружность	Рисунок 96
	диаметром d, равным действитель-

ной величине диаметра изображаемой окружности, и находят точки n пересечения этой окружности с аксонометрическими осями х и у.

Из точек О1, О2 пересечения вспомогательной окружности с осью z, как

из центров радиусом R = О1n= О2n , проводят две дуги nDn и пСп окружности, принадлежащие овалу.

	Из центра О радиусом ОС,
	равным половине малой оси овала,
	засекают на большой оси овала	АВ
	точки О3 и О4. Из этих точек
	радиусом r = О31 = О32 = О43	=
	О44 проводят две дуги. Точки 1, 2, 3
	и 4 сопряжений дуг радиусов R и r
	находят, соединяя точки О1 и О2 с
	точками О3 и О4 и продолжая		Рисунок 97
	прямые до пересечения с дугами
	пСп и nDn.
	Аналогичным образом строят овалы,		расположенные в
	плоскостях, параллельных плоскостям π2,		и π3, (рисунок 98).

Построение овалов, лежащих в плоскостях, параллельных плоскостям π2 и π3, начинают с проведения горизонтальной АВ и вертикальной СD осей овала:

-АВ оси x для овала, лежащего в плоскости, параллельной плоскостям π3;

-АВ оси y для овала, лежащего в плоскости, параллельной

плоскостям π2; Дальнейшие построения овалов аналогичны построениям овала,

лежащего в плоскости, параллельной π1.

Рисунок 98

Прямоугольная диметрия окружности (рис. 99)

На рис. 99 в прямоугольной изометрии изображен куб с ребром α, в грани которого вписаны окружности. Две грани куба изобразятся в виде равных параллелограммов со сторонами 0,94d и 0,47 d, третья грань — в виде ромба со сторонами, равными 0,94d. Две окружности, вписанные в грани куба, проецируются в виде одинаковых эллипсов, третий эллипс по форме близок к окружности.

Направление больших				осей
эллипсов (как и в изометрии)
перпендикулярно		к	соот-
ветствующим аксонометрическим
осям, малые оси параллельны
аксонометрическим осям.
Размер	большой		оси	всех
трех эллипсов равен			d,	т. е.
диаметру окружности,			размеры
малых осей	двух	одинаковых
эллипсов равны d/3		размер малой
оси эллипса, близкого по форме к
окружности,	равен			0,9d.
Практически	при	приведенных
показателях искажения			(1 и	0,5)	Рисунок 99
большие оси всех трех эллипсов

равны 1,06 d, малые оси двух эллипсов равны 0,35 d, малая ось третьего эллипса равна 0,94 d.

Построение эллипсов			в диметрии иногда заменяется более
простым построением овалов (рис. 100)
На рисунке 100		приведены примеры построения диметрических
проекций,	где	эллипсы заменены		овалами,	построенными
упрощенным	способом.		Рассмотрим	пример	построения

диметрической проекции окружности, расположенной параллельно плоскости π2 (рисунок 100, а).

Через точку О проводим оси, параллельные осям х и z. Из центра О радиусом, равным радиусу данной окружности, проводим вспомогательную окружность, которая пересекается с осями в точках 1, 2, 3, 4. Из точек 1 и 3 (по направлению стрелок) проводим горизонтальные линии до пересечения с осями АВ и CD овала и получаем точки О1, О2 , О3, О4. Приняв за центры точки О1, О4, радиусом R проводим дуги 1 2 и 3 4. Приняв за центры точки О2, О3, проводим радиусом R1 замыкающие овал дуги.

Разберем упрощенное построение диметрической проекции окружности, лежащей в плоскости π1 (рисунок 100, в).

Через намеченную точку О проводим прямые, параллельные осям х и y, а также большую ось овала АВ перпендикулярно малой оси CD. Из центра О радиусом, равным радиусу данной окружности, проводим вспомогательную окружность и получаем точки n и n1.

На прямой, параллельной оси z, вправо и влево от центра O

откладываем отрезки, равные диаметру вспомогательной окружности, и получаем точки О1 и О2. Приняв эти точки за центры, проводим радиусом R = О1n1 дуги овалов. Соединяя точки О2 прямыми с концами дуги n1n2, на линии большой оси АВ овала получим точки О4 и О3. Приняв их за центры, проводим радиусом R1 замыкающие овал дуги.

Рисунок 100

3.5 Аксонометрия геометрического тела

Аксонометрия шестигранной призмы (рис.101)

В основании прямой призмы лежит правильный шестиугольник

Изометрическая проекция — Википедия

Стол в прямоугольной изометрической проекции

Изометри́ческая прое́кция (др.-греч. ἴσος «равный» + μετρέω «измеряю») — это разновидность аксонометрической проекции, при которой в отображении трёхмерного объекта на плоскость коэффициент искажения (отношение длины спроецированного на плоскость отрезка, параллельного координатной оси, к действительной длине отрезка) по всем трём осям один и тот же. Слово «изометрическая» в названии проекции пришло из греческого языка и означает «равный размер», отражая тот факт, что в этой проекции масштабы по всем осям равны. В других видах проекций это не так.

Изометрическая проекция используется в машиностроительном черчении и САПР для построения наглядного изображения детали на чертеже, а также в компьютерных играх для трёхмерных объектов и панорам.

Необходимо отметить, что параллельные проекции, разновидностью которых являются аксонометрические и, в том числе, изометрические проекции, делятся также на ортогональные (перпендикулярные), с направлением проекции перпендикулярным к плоскости проекции, и косоугольные, с углом между направлением и плоскостью, отличным от прямого. По советским стандартам (см. ниже) аксонометрические проекции могут быть и ортогональными, и косоугольными^[1]. В результате, по западным стандартам изометрическая проекция определяется более узко и, помимо равенства масштабов по осям, включает условие равенства 120° углов между проекциями любой пары осей. Во избежание путаницы далее, если не указано иное, под изометрической проекцией будет подразумеваться только прямоугольная изометрическая проекция.

• 

  …прямоугольной

• 

  …косоугольной фронтальной

• 

  …косоугольной горизонтальной

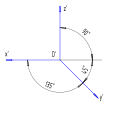
Прямоугольная (ортогональная) изометрическая проекция[править | править код]

В прямоугольной изометрической проекции аксонометрические оси образуют между собой углы в 120°, ось Z’ направлена вертикально. Коэффициенты искажения (kx,ky,kz{\displaystyle k_{x},k_{y},k_{z}}) имеют числовое значение 23≈0,82{\displaystyle {\sqrt {\frac {2}{3}}}\approx 0{,}82}. Как правило, для упрощения построений изометрическую проекцию выполняют без искажений по осям, то есть коэффициент искажения принимают равным 1, в этом случае получают увеличение линейных размеров в 10,82≈1,22{\displaystyle {\frac {1}{0{,}82}}\approx 1{,}22} раза.

Приближённо аксонометрические оси прямоугольной проекции можно построить, если принять tg 30°=4/7 (0,577 и 0,571 соотв.).

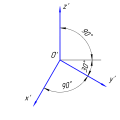
Косоугольная фронтальная изометрическая проекция[править | править код]

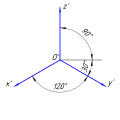
Ось Z’ направлена вертикально, угол между осью X’ и Z’ равен 90°, ось Y’ с углом наклона 135° (допускается 120° и 150°) от оси Z’.

Фронтальная изометрическая проекция выполняется по осям X’, Y’ и Z’ без искажения.

Кривые, параллельные фронтальной плоскости, проецируются без искажений.

Косоугольная горизонтальная изометрическая проекция[править | править код]

Ось Z’ направлена вертикально, между осью Z’ и осью Y’ угол наклона равен 120° (допускается 135° и 150°), при этом сохраняется угол между осями X’ и Y’ равным 90°.

Горизонтальную изометрическую проекцию выполняют без искажения по осям X’, Y’ и Z’.

Кривые, параллельные горизонтальной плоскости^[2] проецируются без искажений.

Стоит отметить, что, поскольку ортогональный трёхгранник невозможно повернуть так, чтобы два его ребра были бы видны взаимно-перпендикулярными, и третье ребро при этом не проецировалась бы в точку, все проекции, в которых видны все три оси.

Изометрический вид объекта можно получить, выбрав направление обзора таким образом, чтобы углы между проекцией осей x, y, и z были одинаковы и равны 120°. К примеру, если взять куб, это можно выполнить направив взгляд на одну из граней куба, после чего повернув куб на ±45° вокруг вертикальной оси и на ±arcsin (tan 30°) ≈ 35,264° вокруг горизонтальной оси. Обратите внимание: на иллюстрации изометрической проекции куба контур проекции образует правильный шестиугольник — все рёбра равной длины и все грани равной площади.

Подобным же образом изометрический вид может быть получен, к примеру, в редакторе трёхмерных сцен: начав с камерой, выровненной параллельно полу и координатным осям, её нужно повернуть вниз на ≈35.264° вокруг горизонтальной оси и на ±45° вокруг вертикальной оси.

Другой путь визуализации изометрической проекции заключается в рассмотрении вида кубической комнаты с верхнего угла с направлением взгляда в противолежащий нижний угол. Ось x здесь направлена диагонально вниз и вправо, ось y — диагонально вниз и влево, ось z — прямо вверх. Глубина также отражается высотой картинки. Линии, нарисованные вдоль осей, имеют угол 120° между собой.

Имеется 8 различных вариантов получения изометрической проекции в зависимости от того, в какой октант смотрит наблюдатель. Изометрическое преобразование точки ax,y,z{\displaystyle a_{x,y,z}} в трёхмерном пространстве в точку bx,y{\displaystyle b_{x,y}} на плоскости при взгляде в первый октант может быть математически описано с помощью матриц поворота следующим образом. Вначале, как объяснено в разделе Визуализация, выполняется поворот вокруг горизонтальной оси (здесь x) на α = arcsin (tan 30°) ≈ 35,264° и вокруг вертикальной оси (здесь y) на β = 45°:

[cxcycz]=[1000cos⁡αsin⁡α0−sin⁡αcos⁡α][cos⁡β0−sin⁡β010sin⁡β0cos⁡β][axayaz]=16[30−31212−22][axayaz]{\displaystyle {\begin{bmatrix}\mathbf {c} _{x}\\\mathbf {c} _{y}\\\mathbf {c} _{z}\\\end{bmatrix}}={\begin{bmatrix}1&0&0\\0&{\cos \alpha }&{\sin \alpha }\\0&{-\sin \alpha }&{\cos \alpha }\\\end{bmatrix}}{\begin{bmatrix}{\cos \beta }&0&{-\sin \beta }\\0&1&0\\{\sin \beta }&0&{\cos \beta }\\\end{bmatrix}}{\begin{bmatrix}\mathbf {a} _{x}\\\mathbf {a} _{y}\\\mathbf {a} _{z}\\\end{bmatrix}}={\frac {1}{\sqrt {6}}}{\begin{bmatrix}{\sqrt {3}}&0&-{\sqrt {3}}\\1&2&1\\{\sqrt {2}}&-{\sqrt {2}}&{\sqrt {2}}\\\end{bmatrix}}{\begin{bmatrix}\mathbf {a} _{x}\\\mathbf {a} _{y}\\\mathbf {a} _{z}\\\end{bmatrix}}}

Затем применяется ортогональная проекция на плоскость x-y:

[bxby0]=[100010000][cxcycz]{\displaystyle {\begin{bmatrix}\mathbf {b} _{x}\\\mathbf {b} _{y}\\0\\\end{bmatrix}}={\begin{bmatrix}1&0&0\\0&1&0\\0&0&0\\\end{bmatrix}}{\begin{bmatrix}\mathbf {c} _{x}\\\mathbf {c} _{y}\\\mathbf {c} _{z}\\\end{bmatrix}}}

Другие семь возможных видов получаются поворотом к противостоящим сторонам и/или инверсией направления взгляда.^[3]

Ограничения аксонометрической проекции[править | править код]

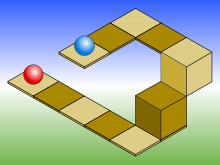Изометрический рисунок с голубым шаром на два уровня выше красного

Как и в других видах параллельных проекций, объекты в аксонометрической проекции не выглядят больше или меньше при приближении или удалении от наблюдателя. Это полезно в архитектурных чертежах и удобно в спрайто-ориентированных компьютерных играх, но, в отличие от перспективной (центральной) проекции, приводит к ощущению искривления, поскольку человеческий глаз или фотография работают иначе.

Это также легко приводит к ситуациям, когда глубину и высоту невозможно оценить, как показано на иллюстрации справа. В этом изометрическом рисунке голубой шар на два уровня выше красного, но это нельзя увидеть, если смотреть только на левую половину картинки. Если выступ, на котором находится голубой шар, расширить на один квадрат, то он окажется точно рядом с квадратом, на котором находится красный шар, создавая оптическую иллюзию, будто оба шара на одном уровне.

Дополнительная проблема, специфичная для изометрической проекции — сложность определения, какая сторона объекта наблюдается. При отсутствии теней и для объектов, которые относительно перпендикулярны и соразмерны, сложно определить, какая сторона является верхней, нижней или боковой. Это происходит из-за приблизительно равных по размеру и площади проекций такого объекта.

Большинство современных компьютерных игр избегают этого за счёт отказа от аксонометрической проекции в пользу перспективного трёхмерного рендеринга. Однако эксплуатация проекционных иллюзий популярна в оптическом искусстве — таком, как работы из серии «невозможной архитектуры» Эшера. Водопад (1961) — хороший пример, в котором строение в основном изометрическое, в то время как блеклый фон использует перспективную проекцию. Другое преимущество заключается в том, что в черчении даже новички легко могут строить углы в 60° с помощью только циркуля и линейки.

Изометрическая проекция в компьютерных играх и пиксельной графике[править | править код]

Рисунок телевизора в почти-изометрической пиксельной графике. У пиксельного узора видна пропорция 2:1

В области компьютерных игр и пиксельной графики аксонометрическая проекция была весьма популярна в силу лёгкости, с которой двухмерные спрайты и плиточная графика могли быть использованы для представления трёхмерной игровой среды — поскольку во время перемещения по игровому полю объекты не меняют размер, компьютеру не требуется масштабировать спрайты или выполнять вычисления, необходимые для моделирования зрительной перспективы. Это позволяло старым 8-битным и 16-битным игровым системам (и, позднее, портативным игровым системам) легко отображать большие трёхмерные пространства. И хотя неразбериха с глубиной (см. выше) иногда могла быть проблемой, хороший дизайн игры способен её смягчить. С приходом более мощных графических систем аксонометрическая проекция стала терять свои позиции.

Проекция в компьютерных играх обычно несколько отличается от «истинной» изометрической в силу ограничений растровой графики — линии по осям x и y не имели бы аккуратного пиксельного узора, если бы рисовались под углом в 30° к горизонтали. Хотя современные компьютеры могут устранять эту проблему с помощью сглаживания, ранее компьютерная графика не поддерживала достаточную цветовую палитру или не располагала достаточной мощностью процессоров для его выполнения. Вместо этого использовалась пропорция пиксельного узора 2:1 для рисования осевых линий x и y, в результате чего эти оси располагались под углом arctg 0,5 ≈ 26,565° к горизонтали. (Игровые системы с неквадратными пикселями могли, однако, приводить к другим углам, включая полностью изометрические^[4]). Поскольку здесь из трёх углов между осями (116,565°, 116,565°, 126,87°) равны только два, такой вид проекции более точно характеризуется как вариация диметрической проекции. Однако большинство представителей сообществ компьютерных игр и растровой графики продолжает называть эту проекцию «изометрической перспективой». Также, часто используются термины «вид 3/4 (англ.)» и «2.5D».

Термин применялся и к играм, не использующим пропорцию 2:1, общую для многих компьютерных игр. Fallout^[5] и SimCity 4^[6], в которых используется триметрическая проекция, были отнесены к «изометрическим». Игры с косоугольной проекцией, такие как The Legend of Zelda: A Link to the Past^[7] и Ultima Online^[8], а также игры с перспективной проекцией с видом «с воздуха» (англ.)русск., такие как The Age of Decadence (англ.)^[9] и Silent Storm^[10], также иногда относят к изометрическим или «псевдо-изометрическим».

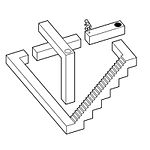Кадр из игры «echochrome»

Интересный пример использования особенностей изометрической проекции наблюдается в игре echochrome (яп. 無限回廊 муген кайро:). Слоган игры — «В этом мире то, что ты видишь, становится реальностью». Смысл игры заключается в том, что иллюзия, возникающая при взгляде на изометрически построенный трёхмерный уровень с определённой точки, перестаёт быть иллюзией. Например, если посмотреть на уровень таким образом, чтобы площадки, находящиеся на разной высоте, выглядели так, будто они находятся на одной и той же высоте (см. изображение с синим и красным шарами из предыдущего раздела), игрой они будут расцениваться как находящиеся на одной высоте, и человек (игрок) сможет запросто «перешагнуть» с одной площадки на другую. Затем, если повернуть карту уровня и посмотреть на конструкцию так, чтобы было отчётливо видно разницу в высоте, можно понять, что в действительности человек «перешагнул» на другую высоту, пользуясь тем, что изометрическая иллюзия на какой-то момент стала реальностью. На приведённом в качестве иллюстрации кадре из игры положение площадки, находящейся вверху лестницы, можно представить двояко: в одном случае она находится на одной высоте с площадкой, на которой находится игрок (можно перешагнуть), а в другом случае — под ней (можно спрыгнуть через чёрное отверстие). Оба случая будут одновременно являться правдой. Очевидно, этот эффект достигается отсутствием перспективы в изометрии.

История изометрических компьютерных игр[править | править код]

Q*bert (1982), одна из первых игр с изометрической графикой

Первыми играми, использующими изометрическую проекцию, были аркадные игры начала 1980-х: так, Q*bert^[11] и Zaxxon^[12] выпущены в 1982 году. Q*bert показывает статичную пирамиду, нарисованную в изометрической перспективе, по которой должен прыгать управляемый игроком персонаж. Zaxxon предлагает прокручиваемые изометрические уровни, над которыми летает управляемый игроком самолётик. Год спустя, в 1983 году, была выпущена аркадная игра Congo Bongo (англ.)^[13], работавшая на тех же игровых автоматах, что и Zaxxon. В этой игре персонаж перемещается по большим изометрическим уровням, включающим трёхмерные подъёмы и спуски. То же самое предлагается и в аркадной игре Marble Madness (1984).

С выходом Ant Attack (англ.) (1983) для ZX Spectrum изометрические игры перестали быть изюминкой только аркадных игровых автоматов и пришли также и в домашние компьютеры. Журнал CRASH присудил этой игре 100 % в категории «графика» за новую «трёхмерную» технологию.^[14] Год спустя для ZX была выпущена игра Knight Lore, которая расценивается как революционное произведение^[15], определившее последующий жанр изометрических квестовых игр^[16]. На домашних компьютерах было отмечено столько изометрических игр-последователей Knight Lore, что эта игра стала считаться вторым наиболее клонируемым образцом программного обеспечения после текстового редактора WordStar (англ.).^[17] Среди клонов большой успех имела игра Head Over Heels (1987)^[18]. Однако, изометрическая проекция не ограничивалась только аркадами и квестовыми играми — например, стратегическая игра Populous (1989) также использовала изометрическую перспективу.

На протяжении 1990-х некоторые очень успешные игры вроде Civilization II и Diablo использовали фиксированную изометрическую перспективу. С приходом 3D ускорителей на персональные компьютеры и игровые консоли игры с трёхмерной перспективой в основном переключились на полноценную трёхмерность вместо изометрической перспективы. Это можно видеть в преемницах вышеназванных игр — начиная с Civilization IV в этой серии используется полная трёхмерность. Diablo II, как и ранее, использует фиксированную перспективу, но опционально применяет перспективное масштабирование спрайтов на расстоянии, получая псевдо-трёхмерную перспективу.^[19]

1. ↑ ^{1 2} По ГОСТ 2.317-69 — Единая система конструкторской документации. Аксонометрические проекции.
2. ↑ Здесь горизонтальной называется плоскость, перпендикулярная оси Z (которая является прообразом оси Z’).
3. ↑ Ingrid Carlbom, Joseph Paciorek. Planar Geometric Projections and Viewing Transformations // ACM Computing Surveys (CSUR) : журнал. — ACM, декабрь 1978. — Т. 10, № 4. — С. 465—502. — ISSN 0360-0300. — DOI:10.1145/356744.356750.
4. ↑ Так, в распространённом разрешении CGA/VGA 320×200 этот угол равняется arctg 0,6 ≈ 30,96°.
5. ↑ Jeff Green. GameSpot Preview: Arcanum (англ.) (недоступная ссылка). GameSpot (29 февраля 2000). Дата обращения 29 сентября 2008. Архивировано 31 августа 2000 года.
6. ↑ Steve Butts. SimCity 4: Rush Hour Preview (англ.). IGN (9 сентября 2003). Дата обращения 29 сентября 2008. Архивировано 19 февраля 2012 года.
7. ↑ GDC 2004: The History of Zelda (англ.). IGN (25 марта 2004). Дата обращения 29 сентября 2008. Архивировано 19 февраля 2012 года.
8. ↑ Dave Greely, Ben Sawyer. Has Origin Created the First True Online Game World? (англ.). Gamasutra (19 августа 1997). Дата обращения 29 сентября 2008. Архивировано 19 февраля 2012 года.
9. ↑ Age of Decadence (англ.). Iron Tower Studios. Дата обращения 29 сентября 2008. Архивировано 19 февраля 2012 года.
10. ↑ Steve O’Hagan. PC Previews: Silent Storm (англ.). GamesRadar—CVG (7 августа 2003). Дата обращения 29 сентября 2008. Архивировано 19 февраля 2012 года.
11. ↑ Q*bert (англ.) на сайте Killer List of Videogames
12. ↑ Zaxxon (англ.) на сайте Killer List of Videogames
13. ↑ Congo Bongo (англ.) на сайте Killer List of Videogames
14. ↑ Soft Solid 3D Ant Attack // CRASH : журнал. — февраль 1984. — № 1.
15. ↑ Ultimate Play The Game — Company Lookback // Retro Micro Games Action — The Best of gamesTM (англ.) Retro. — Highbury Entertainment, 2006. — Т. 1. — С. 25.
16. ↑ Steven Collins. Game Graphics During the 8-bit Computer Era // ACM SIGGRAPH. Computer Graphics. — май 1998. — Т. 32, № 2. Архивировано 9 сентября 2012 года.
17. ↑ Krikke J. Axonometry: a matter of perspective // IEEE. Computer Graphics and Applications. — июль-август 2000. — Т. 20, № 4. — С. 7—11. — DOI:10.1109/38.851742.
18. ↑ Looking for an old angle // CRASH : журнал. — апрель 1988. — № 51.
19. ↑ Diablo II Nears Completion As Blizzard Prepares For Final Phase Of Beta Testing (неопр.) (недоступная ссылка). Market Wire (май 2000). Дата обращения 29 сентября 2008. Архивировано 10 июля 2012 года.

• Introduction to 3 Dimensional graphics (англ.) (недоступная ссылка). Blueprint project. IDER group, Manufactuing Systems Engineering Centre, University of Hertfordshire. — Пояснения и учебник по рисованию в изометрической перспективе из Хертфорширдского университета. Дата обращения 29 сентября 2008. Архивировано 28 октября 2000 года.
• Herbert Glarner. Isometric Projection (англ.) (19 марта 2007). Дата обращения 29 сентября 2008. Архивировано 19 февраля 2012 года.
• PixelDam (англ.). — A collaborative pixelart community. Дата обращения 29 сентября 2008. Архивировано 19 февраля 2012 года.
• Tom Gersic. Rendering Isometric Tiles in Blender 3D (англ.). — Учебник с примерами по созданию изометрических плиток в программе Blender 3D. Дата обращения 29 сентября 2008. Архивировано 19 февраля 2012 года.

• Богданов В. Н., Малежик И. Ф., Верхола А. П. и др. Справочное руководство по черчению. — М.: Машиностроение, 1989. — С. 864. — ISBN 5-217-00403-7.
• Фролов С. А. Начертательная геометрия. — 2-е изд., перераб. и доп. — М.: Машиностроение, 1983. — С. 240.

Аксонометрия в Автокаде: практический пример

Аксонометрия в Автокаде может быть создана различными способами, однако давайте рассмотри наиболее простой вариант без привлечения в работу сторонних приложений. Это способ может быть полезен проектировщикам различных инженерных систем.

Аксонометрические схемы в Автокаде

Вопрос на ответ «Как сделать аксонометрию в Автокаде?» мне подсказал мой читатель, Семенов Максим (Этот адрес электронной почты защищён от спам-ботов. У вас должен быть включен JavaScript для просмотра.), который на практике использует нижеприведенный способ.

Инженерная аксонометрия в AutoCAD начинается с чертежа плана, который должен содержать коммуникационные сети. Рекомендуется все построения выполнять на отдельных тематических слоях, так как если ваши инженерные сети начерчены в отдельном слое Автокад, то появляется возможность быстрого их выделения через операцию «Быстрый выбор».

В качестве примера рассмотрим произвольный набор примитивов, которые будут аналогом реальной инженерной сети.

Алгоритм, как рисовать аксонометрию в AutoCAD

В AutoCAD аксонометрия схемы может быть получена следующим путем:

1. Выделяем систему, копируем в ближайшее место для дальнейшей работы с ней.

2. Поворачиваем схему на 315. Для этого воспользуемся командой Автокад «Поворот».

3. Сделаем из нашей схемы блок AutoCAD.

4. Выделяем созданный блок и в палитре свойств (Ctrl+1) и начинаем превращать его в аксонометрическую схему, для этого потребуется:

– в пункте «Геометрия» изменить параметр «Масштаб Y» на значение 0,4142;

– в пункте «Разное» изменить параметр «Поворот» на значение 22,5.

5. Для того чтобы ваша будущая схема по размерам соответствовала вашим планам необходимо воспользоваться операцией «Масштабирования». Блок увеличим в 1,306569 раз. Далее применяем команду Автокад «Расчленить» и проверяем, сошлись ли у вас размеры и углы.

Рекомендация: для построения быстрых аксонометрических схем высотных зданий советуем создавать динамические блоки Автокад с операцией «Массив». Данная операция дает возможность установки сан. тех приборов на схеме на 1-ом этаже с последующим растяжением на все оставшиеся этажи через заданный промежуток без применения операции копирование.

 

Видео курсы по AutoCAD:

1. Использование AutoCAD на 100%
2. 3D моделирование в AutoCAD
3. Адаптация AutoCAD под стандарты предприятия
4. Советы и хитрости
5. Блоки и поля в AutoCAD

Аксонометрия

Аксонометрия — особый отдел в черчении, в нем изучается то, как получить наглядное изображение предметов на плоскости. Аксонометрическая проекция выглядит как точный рисунок предмета. Аксонометрия, расшифровывается как измерение по осям.

Проекции в аксонометрии разделяют на несколько видов:

1) Прямоугольная — это когда проецируемые прямые, перпендикулярные к плоскости акс.проекции. Так же в этот вод входят — диметрическая и изометрическая.

2) Косоугольная — этом когда прямые идут не под углом 90⁰ относительно акс. проекции. Так же в этот вид входит проекция фронтальная диметрическая.

Во время выполнения переноса предмета на проекцию, возможно искажение осей.

Помощь в ознакомлении с учебником или с любой книгой по которой учатся предоставляет сайт — учебник pdf (http://ruscopybook.com/). Публикация изданий позволяет учителям ознакомиться с существующими учебно-методическими комплектами и выбрать подходящий для преподавания. Родителям — готовые домашние задания.

Чаще всего используются в работе, косоугольная фронтальная диметрическая и изометрическая проекции, потому что они являются наиболее простыми. Их мы и разберем. По другим предметам поможет разобраться сайт учебник pdf (http://ruscopybook.com/).

— Косоугольная фронтальная диметрическая проекция.
для данной проекции искажение на оси у — 0,5, на оси х и z = 0. Это означает что высота и длина отмеряются в натуральные, а ширина отмеряется с уменьшением в два раза.

— Прямоугольная изометрическая проекция
Данная проекция обладает преимуществом так как данные не искажаются на всех осях. То есть имеет одинаковое измерение по всем осям, соответственно и размеры предмета, на осях откладываются натуральные.

Для того что бы получить аксонометрическую проекцию, нужно расположить предмет в системе координатных осей, перед акс.плоскостью. Дать проецируемое направление и провести через все точки мысленно, лучи до пересечения с плоскостью.

— Изометрическая Прямоугольная
Перемещаем предмет в угол координат и ставим его так что бы наклон сторон был равным к акс. плоскости. Проводим невидимые лучи через точки, под углом девяносто градусов, до пересечения с плоскостью.

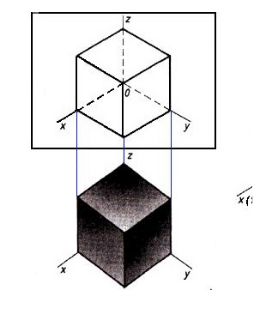
— Косоугольная фронтальная диметрическая проекция.
Рядом с P-плоскостью ставим предмет, чтобы передняя сторона находилась фронтально к плоскости. Проводим лучи параллельные, относительно плоскости под острым углом. Получаем координатные оси и проекцию предмета косоугольную фронтальную диметрическую.

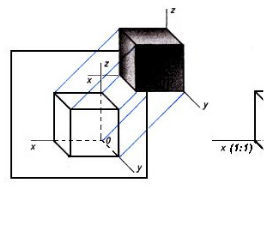
Для чего нужно уметь правильно переносить плоские фигуры на проекцию?
Плоской фигурой называются те фигуры у которых точки входят в одну плоскость. На пример — прямоугольник, ромб, квадрат и другие. Умение строить на проекции треугольник, квадраты, трапецию и шестиугольников очень нужно для того чтобы построить модели, детали и проекции геометрического тела.

---

Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:

---