Окружность, круг, сегмент, сектор. Формулы и свойства

Определение. Окружность — это совокупность всех точек на плоскости, которые находятся на одинаковом расстоянии от заданной точки О, которая называется центром окружности.

Определение. Единичная окружность — окружность, радиус которой равна единице.

Определение. Круг — часть плоскости, ограничена окружностью.

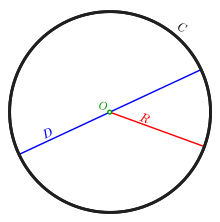
Определение. Радиус окружности R — расстояние от центра окружности О до любой точки окружности.

Определение. Диаметр окружности D — отрезок, который соединяет две точки окружности и проходит через ее центр.

Основные свойства окружности

1. Диаметр окружности равен двум радиусам.

D = 2r

2. Кратчайшее расстояние от центра окружности к секущей (хорде) всегда меньше радиуса.

3. Через три точки, которые не лежат на одной прямым, можно провести только одну окружность.

4. Среди всех замкнутых кривых с одинаковой длиной, окружность имеет наибольшую площадь.

5. Если две окружности соприкасаются в одной точке, то эта точка лежит на прямой, что проходит через центры этих окружностей.

Формулы длины окружности и площади круга

Формулы длины окружности

1. Формула длины окружности через диаметр:

L = πD

2. Формула длины окружности через радиус:

L = 2πr

Формулы площади круга

1. Формула площади круга через радиус:

S = πr²

2. Формула площади круга через диаметр:

S = πD²4

Уравнение окружности

1. Уравнение окружности с радиусом r и центром в начале декартовой системы координат:

r² = x² + y²

2. Уравнение окружности с радиусом r и центром в точке с координатами (a, b) в декартовой системе координат:

r

2 = (x — a)² + (y — b)²

3. Параметрическое уравнение окружности с радиусом r и центром в точке с координатами (a, b) в декартовой системе координат:

{	x = a + r cos t
	y = b + r sin t

Касательная окружности и ее свойства

Определение. Касательная окружности — прямая, которая касается окружности только в одной точке.

Основные свойства касательных к окружности

1. Касательная всегда перпендикулярна к радиусу окружности, проведенного в точке соприкосновения.

2. Кратчайшее расстояние от центра окружности к касательной равна радиусу окружности.

3. Если две касательные, с точками соприкосновения B и C, на одной окружности не параллельны, то они пересекаются в точке A, а отрезок между точкой соприкосновения и точкой пересечения одной касательной равен таком же отрезке на другой касательной:

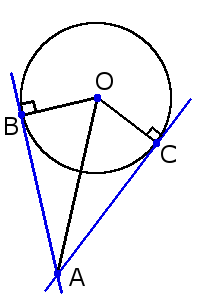
AB = AC

Также, если провести прямую через центр окружности О и точку пересечения A этих касательных, то углы образованный между этой прямой и касательными будут равны:

∠ОAС = ∠OAB

Секущая окружности и ее свойства

Определение. Секущая окружности — прямая, которая проходит через две точки окружности.

Основные свойства секущих

1. Если с точки вне окружности (Q) выходят две секущие, которые пересекают окружность в двух точках A и B для одной секущей и C и D для другой секущей, то произведения отрезков двух секущих равны между собою:

AQ ∙ BQ = CQ ∙ DQ

2. Если из точки Q вне окружности выходит секущая прямая, что пересекает окружность в двух точках A и B, и касательная с точкой соприкосновения C, то произведение отрезков секущей равна квадрату длины отрезка касательной:

AQ ∙ BQ = CQ²

Хорда окружности ее длина и свойства

Определение. Хорда окружности — отрезок, который соединяет две точки окружности.

Длина хорды

1. Длина хорды через центральный угол и радиус:

AB = 2r sin α2

2. Длина хорды через вписанный угол и радиус:

AB = 2r sin α

Основные свойства хорд

1. Две одинаковые хорды стягивают две одинаковые дуги:

если хорды AB = CD, то

дуги ◡ AB = ◡ CD

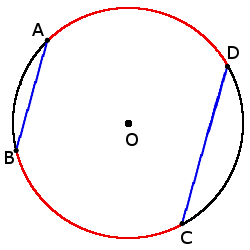2. Если хорды параллельные, то дуги между ними будут одинаковые:

если хорды AB ∣∣ CD, то

◡ AD = ◡ BC

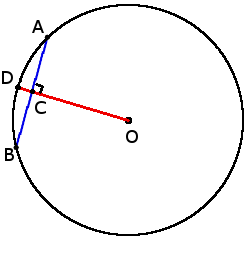3. Если радиус окружности перпендикулярен к хорде, то он разделяет хорду пополам в точке их пересечения:

если OD ┴ AB, то

AC = BC

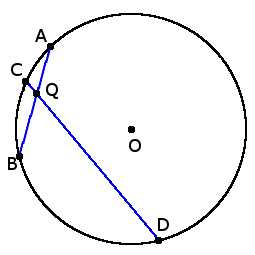4. Если две хорды AB и CD пересекаются в точке Q, то произведение отрезков, что образовались при пересечении, одной хорды равны произведению отрезков другой хорды:

AQ ∙ BQ = DQ ∙ QC

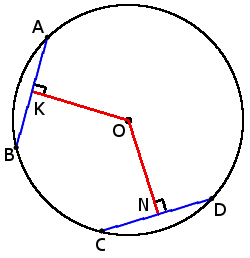5. Хорды с одинаковой длиной находятся на одинаковом расстоянии от центра окружности.

если хорды AB = CD, то

ON = OK

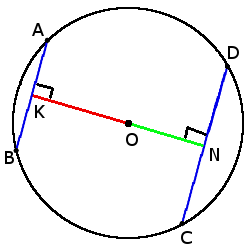6. Чем больше хорда тем ближе она к центру.

если CD > AB, то

ON < OK

Центральный угол, вписанный угол и их свойства

Определение. Центральный угол окружности — угол, вершиной которого есть центр окружности.

Определение. Угол вписанный в окружность — угол, вершина которого лежит на окружности, а стороны угла пересекают окружность.

Основные свойства углов

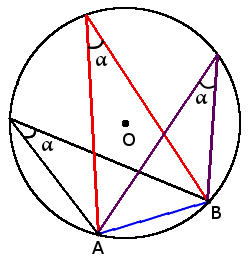1. Все вписанные углы, которые опираются на одну дугу — равны.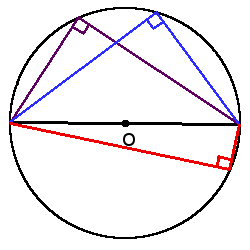 2. Вписанний угол, который опирается на диаметр будет прямым (90°). 3. Вписанный угол равен половине центрального угла, что опирается на ту же дугу

β = α2

4. Если два вписанных угла опираются на одну хорду и находятся по различные стороны от нее, то сумма этих углов равна 180°.

α + β = 180°

Определение. Дуга окружности (◡) — часть окружности, которая соединяет две точки на окружности.

Определение. Градусная мера дуги — угол между двумя радиусами, которые ограничивают эту дугу. Градусная мера дуги всегда равна градусной мере центрального угла, который ограничивает эту дугу своими сторонами.

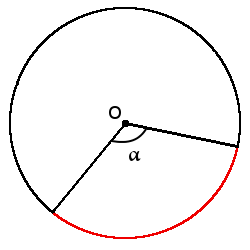Формула длины дуги через центральный угол (в градусах):

l = πr180°∙ α

Определение. Полуокружность — дуга в которой концы соединены диаметром окружности.

Определение. Полукруг (◓) — часть круга, которая ограничена полуокружностью и диаметром.

Определение. Сектор (◔) — часть круга, которая ограничена двумя радиусами и дугой между этими радиусами.

Формула. Формула площади сектор через центральный угол (в градусах)

S = πr²360°∙ α

Определение. Сегмент — часть круга, которая ограничена дугой и хордой, что соединяет ее концы.

Определение. Концентрические окружности — окружности с различными радиусами, которые имеют общий центр.

Определение. Кольцо — часть плоскости ограниченная двумя концентрическими окружностями.

Окружность — Википедия

Окружность (C), её центр (O), радиус (R) и диаметр (D)

Окру́жность — замкнутая плоская кривая, которая состоит из всех точек на плоскости, равноудалённых от заданной точки^[1]: эта точка называется центром окружности. Отрезок, соединяющий центр с какой-либо точкой окружности, называется радиусом; радиусом называется также и длина этого отрезка. Окружность разбивает плоскость на две части^[2] — конечную внутреннюю и бесконечную внешнюю. Внутренность окружности называется кругом; граничные точки (то есть саму окружность) в зависимости от подхода, круг может включать или не включать.

Построение окружности циркулем

Практическое построение окружности возможно с помощью циркуля.

Окружность нулевого радиуса (вырожденная окружность) является точкой, далее этот случай исключается из рассмотрения, если не оговорено иное.

Окружность называется единичной, если её радиус равен единице. Единичная окружность является одним из основных объектов тригонометрии.

Далее всюду буква R{\displaystyle R} обозначает радиус окружности.

Прямая может иметь с окружностью не более двух общих точек.

Прямая, пересекающая окружность в двух различных точках, называется секущей. Отрезок секущей, расположенный внутри окружности, называется хордой. Хорда, проходящая через центр окружности, называется диаметром; тот же термин используется для его длины. Диаметр вдвое больше радиуса: D=2R,{\displaystyle D=2R,} он делит окружность на две равные части и поэтому является её осью симметрии. Диаметр больше любой другой хорды^[3].

Хорда разбивает круг на две части, называемые сегментами круга. Два различных радиуса тоже разбивают круг на две части, называемые секторами круга (см. рисунки)^[3].

Любые две несовпадающие точки окружности делят её на две части. Каждая из этих частей называется дугой окружности. Дуга называется полуокружностью, если отрезок, соединяющий её концы, является диаметром.

Для заданной окружности имеют место следующие свойства^[3].

• Хорды, равноотстоящие от центра, равны. Обратно, если две хорды равны по длине, то они одинаково удалены от центра.
• Равным хордам соответствуют равные дуги, и наоборот.

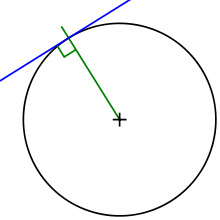
Прямая, имеющая с окружностью ровно одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности. Касательная к окружности всегда перпендикулярна её радиусу (и диаметру), проведенному в точке касания. То есть радиус является одновременно и нормалью к окружности^[4].

Отрезки касательных к окружности, проведённых из одной точки, не лежащей на окружности, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности^[5].

• 

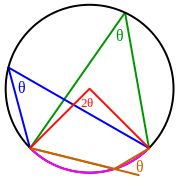
  Вписанный угол θ равен половине величины центрального угла 2θ, опирающегося на ту же самую дугу (розового цвета)

• 

  К расчёту длины дуги и хорды

Центральный угол — угол с вершиной в центре окружности. Центральный угол может быть принят как угловая мера дуги, на которую он опирается. Центральный угол, образуемый дугой окружности, равной по длине радиусу, в математике принимается в качестве единицы измерения углов, и называется радиан.

Из определения радиана следует, что длина L{\displaystyle L} любой дуги окружности связана с центральным углом θ{\displaystyle \theta }, опирающимся на эту дугу, простым соотношением^[6]: L=Rθ.{\displaystyle L=R\theta .} (при этом длина хорды, стягивающей ту же дугу, равна 2Rsin⁡θ2<L{\displaystyle 2R\sin {\theta \over 2}<L}). Поскольку длина окружности равна 2πR{\displaystyle 2\pi R}, с ростом угла значение его радианной меры меняется от 0 до 2π.{\displaystyle 2\pi .}

Вписанный угол — угол, вершина которого лежит на окружности, а стороны пересекают эту окружность.

Внешний угол для вписанного угла — угол, образованный одной стороной и продолжением другой стороны вписанного угла (угол θ коричневого цвета на рис.). Внешний угол для вписанного угла равен вписанному углу, опирающемуся на ту же хорду с другой стороны.

Угол между окружностью и прямой — угол между секущей прямой и одной из двух касательных к окружности в точке пересечения прямой и окружности.

Свойства вписанных углов:

• Вписанный угол либо равен половине центрального угла, опирающегося на его дугу, либо дополняет половину этого угла до 180°. Вписанный угол, опирающийся на дугу длиной в половину окружности, всегда прямой (равен 90°).
• Вписанный угол не меняет своей величины при перемещении его вершины вдоль окружности.
• Два вписанных угла, опирающиеся на одну и ту же дугу, равны.

Другие свойства:

• Угол между двумя секущими, проведёнными из точки, лежащей вне окружности, равен полуразности мер дуг, лежащих между секущими.
• Угол между пересекающимися хордами равен полусумме мер дуги, лежащей в угле, и дуги напротив неё.
• Угол между касательной и хордой, имеющими общую точку, равен половине угловой меры дуги, стягиваемой хордой.

• Изопериметрическое неравенство: Из всех замкнутых кривых данной длины окружность ограничивает область максимальной площади.
• Через три точки, не лежащие на одной прямой, можно провести окружность, и притом только одну.
• Говорят, что две окружности касаются, если они имеют единственную общую точку. Точка касания двух окружностей лежит на прямой, проходящей через их центры.
• Теорема о секущих: Если через произвольную точку E{\displaystyle E} проведена секущая, то произведение расстояний от этой точки до точек пересечения секущей с окружностью не зависит от выбора секущей (и равно абсолютной величине степени точки относительно окружности). Если точка E{\displaystyle E} лежит вне окружности, то из нее к окружности можно провести касательную. Квадрат длины отрезка касательной до точки касания будет равен той же величине.

• Как частный случай предыдущего, при пересечении двух хорд в произвольной точке E{\displaystyle E} получаются отрезки, произведение длин которых у одной хорды равно соответствующему произведению у другой (см. рисунок), т. е. AE⋅EB=CE⋅ED{\displaystyle AE\cdot EB=CE\cdot ED}.

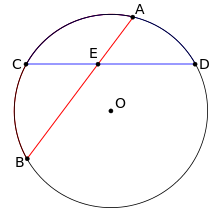AE⋅EB=CE⋅ED{\displaystyle AE\cdot EB=CE\cdot ED} Если радиус круга равен 1, то его окружность равна 2π.

Длина окружности:

C=2πR=πD.{\displaystyle C=2\pi R=\pi D.}

Радиус окружности:

R=C2π=D2.{\displaystyle R={\frac {C}{2\pi }}={\frac {D}{2}}.}

Диаметр окружности:

D=Cπ=2R.{\displaystyle D={\frac {C}{\pi }}=2R.}

Площадь круга радиуса R:

S=πR2=πD24.{\displaystyle S=\pi R^{2}={\frac {\pi D^{2}}{4}}.}

Площадь сектора, ограниченного центральным углом α, измеряемым в градусах, радиусом R:

S=πR2α360∘.{\displaystyle S=\pi R^{2}{\frac {\alpha }{360^{\circ }}}.}

Площадь сегмента, ограниченного дугой окружности, центральным углом α, хордой:

S=πR2α360∘−R2sin⁡α2.{\displaystyle S=\pi R^{2}{\frac {\alpha }{360^{\circ }}}-{\frac {R^{2}\sin \alpha }{2}}.}

Окружность, наряду с прямой, является самой распространённой кривой практически во всех областях человеческой деятельности. История её исследования и применения уходит в глубокую древность; особенную важность придало этой теме изобретение колеса. Античные учёные рассматривали прямые и окружности как единственный пример «совершенных» кривых, поэтому в геометрии считались допустимыми только построения с помощью циркуля и линейки, а движение планет моделировалось как наложение вращений по окружностям. Теории окружностей посвящена III книга «Начал» Евклида.

Также в древности было открыто, что отношение длины окружности к её диаметру (число π) одно и то же для всех окружностей. Исторически важной темой многовековых исследований было уточнение этого отношения, а также попытки решить проблему «квадратуры круга». В дальнейшем развитие теории окружностей привело к созданию тригонометрии, теории колебаний и многих других практически важных разделов науки и техники.

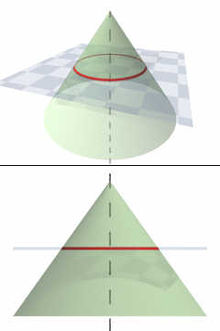Окружность получается как сечение конуса плоскостью, перпендикулярной его оси

Аналитическая геометрия окружностей[править | править код]

С точки зрения аналитической геометрии, окружность является простой плоской алгебраической кривой второго порядка. Окружность является частным случаем эллипса, у которого полуоси равны, и поэтому окружность относится к коническим сечениям.

Декартовы координаты[править | править код]

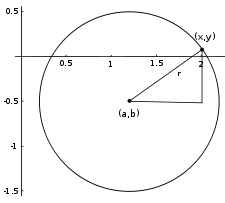Окружность радиуса r = 1, центр (a, b) = (1.2, −0.5)

Общее уравнение окружности записывается как:

x2+y2+Ax+By+C=0,{\displaystyle x^{2}+y^{2}+Ax+By+C=0,}

или

(x−x0)2+(y−y0)2=R2,{\displaystyle \left(x-x_{0}\right)^{2}+\left(y-y_{0}\right)^{2}=R^{2},}

где

2×0=−A,2y0=−B,2R=A2+B2−4C.{\displaystyle 2x_{0}=-A,\;2y_{0}=-B,\;2R={\sqrt {A^{2}+B^{2}-4C}}.}

Точка (x0,y0){\displaystyle \left(x_{0},y_{0}\right)} — центр окружности, R{\displaystyle R} — её радиус.

Уравнение окружности радиуса R{\displaystyle R} с центром в начале координат:

x2+y2=R2.{\displaystyle x^{2}+y^{2}=R^{2}.}

Уравнение окружности, проходящей через точки (x1,y1),(x2,y2),(x3,y3),{\displaystyle \left(x_{1},y_{1}\right),\left(x_{2},y_{2}\right),\left(x_{3},y_{3}\right),} не лежащие на одной прямой (с помощью определителя):

|x2+y2xy1x12+y12x1y11x22+y22x2y21x32+y32x3y31|=0.{\displaystyle {\begin{vmatrix}x^{2}+y^{2}&x&y&1\\x_{1}^{2}+y_{1}^{2}&x_{1}&y_{1}&1\\x_{2}^{2}+y_{2}^{2}&x_{2}&y_{2}&1\\x_{3}^{2}+y_{3}^{2}&x_{3}&y_{3}&1\end{vmatrix}}=0.}

Тогда в явном виде координаты центра окружности определяются по формулам:

x0=−12y1(x22+y22−x32−y32)+y2(x32+y32−x12−y12)+y3(x12+y12−x22−y22)x1(y2−y3)+x2(y3−y1)+x3(y1−y2){\displaystyle x_{0}=-{\frac {1}{2}}{\frac {y_{1}(x_{2}^{2}+y_{2}^{2}-x_{3}^{2}-y_{3}^{2})+y_{2}(x_{3}^{2}+y_{3}^{2}-x_{1}^{2}-y_{1}^{2})+y_{3}(x_{1}^{2}+y_{1}^{2}-x_{2}^{2}-y_{2}^{2})}{x_{1}(y_{2}-y_{3})+x_{2}(y_{3}-y_{1})+x_{3}(y_{1}-y_{2})}}}

y0=12×1(x22+y22−x32−y32)+x2(x32+y32−x12−y12)+x3(x12+y12−x22−y22)x1(y2−y3)+x2(y3−y1)+x3(y1−y2){\displaystyle y_{0}={\frac {1}{2}}{\frac {x_{1}(x_{2}^{2}+y_{2}^{2}-x_{3}^{2}-y_{3}^{2})+x_{2}(x_{3}^{2}+y_{3}^{2}-x_{1}^{2}-y_{1}^{2})+x_{3}(x_{1}^{2}+y_{1}^{2}-x_{2}^{2}-y_{2}^{2})}{x_{1}(y_{2}-y_{3})+x_{2}(y_{3}-y_{1})+x_{3}(y_{1}-y_{2})}}}

Окружность также можно описать с помощью параметрического уравнения:

{x=x0+Rcos⁡φy=y0+Rsin⁡φ,0⩽φ<2π.{\displaystyle {\begin{cases}x=x_{0}+R\cos \varphi \\y=y_{0}+R\sin \varphi \end{cases}},\;\;\;0\leqslant \varphi <2\pi .}

В декартовой системе координат окружность не является графиком функции, но она может быть описана как объединение графиков двух следующих функций:

y=y0±R2−(x−x0)2.{\displaystyle y=y_{0}\pm {\sqrt {R^{2}-(x-x_{0})^{2}}}.}

Если центр окружности совпадает с началом координат, функции принимают вид:

y=±R2−x2.{\displaystyle y=\pm {\sqrt {R^{2}-x^{2}}}.}

Полярные координаты[править | править код]

Окружность радиуса R{\displaystyle R} с центром в точке (ρ0,ϕ0){\displaystyle \left(\rho _{0},\phi _{0}\right)}:

ρ2−2ρρ0cos⁡(ϕ−ϕ0)+ρ02=R2.{\displaystyle \rho ^{2}-2\rho \,\rho _{0}\cos \left(\phi -\phi _{0}\right)+\rho _{0}^{2}=R^{2}.}

Если полярные координаты центра окружности ρ0=R,ϕ0=α,{\displaystyle \rho _{0}=R,\;\phi _{0}=\alpha ,} то проходящая через начало координат окружность описывается уравнением:

ρ(φ)=2Rcos(φ−α),α−π2⩽φ⩽α+π2.{\displaystyle \rho (\varphi )=2R\cos \,(\varphi -\alpha ),\;\;\;\alpha -{\frac {\pi }{2}}\leqslant \varphi \leqslant \alpha +{\frac {\pi }{2}}.}

Если же центр является началом координат, то уравнение будет иметь вид

ρ=R.{\displaystyle \rho =R.}

Комплексная плоскость[править | править код]

На комплексной плоскости окружность задаётся формулой:

|z−z0|=R{\displaystyle \left|z-z_{0}\right|=R}

или в параметрическом виде

z=z0+Reit,t∈R.{\displaystyle z=z_{0}+Re^{it},\,t\in \mathbb {R} .}

Окружности в пространстве[править | править код]

В пространстве окружность радиуса R{\displaystyle R} с центром в точке M0(x0,y0,z0){\displaystyle M_{0}(x_{0},y_{0},z_{0})} можно определить как контур диаметрального сечения сферы

(x−x0)2+(y−y0)2+(z−z0)2=R2{\displaystyle (x-x_{0})^{2}+(y-y_{0})^{2}+(z-z_{0})^{2}=R^{2}}

плоскостью

a⋅(x−x0)+b⋅(y−y0)+c⋅(z−z0)=0{\displaystyle a\cdot (x-x_{0})+b\cdot (y-y_{0})+c\cdot (z-z_{0})=0},

где a,b,c{\displaystyle a,b,c} — параметры, не равные одновременно нулю; то есть все точки, лежащие на данной окружности, есть решения системы

{(x−x0)2+(y−y0)2+(z−z0)2=R2,a⋅(x−x0)+b⋅(y−y0)+c⋅(z−z0)=0.{\displaystyle {\begin{cases}(x-x_{0})^{2}+(y-y_{0})^{2}+(z-z_{0})^{2}=R^{2},\\a{\cdot }(x-x_{0})+b{\cdot }(y-y_{0})+c{\cdot }(z-z_{0})=0.\end{cases}}}

Например, при a=c≠0{\displaystyle a=c\neq 0} решения этой системы можно задать параметрически следующим образом:

{x=x0+Ra2+c2⋅(c⋅cos⁡t−a⋅b⋅sin⁡ta2+b2+c2),y=y0+R⋅a2+c2a2+b2+c2⋅sin⁡t,z=z0−Ra2+c2⋅(a⋅cos⁡t+b⋅c⋅sin⁡ta2+b2+c2),t∈[0;2π).{\displaystyle {\begin{cases}x=x_{0}+{\dfrac {R}{\sqrt {a^{2}+c^{2}}}}\cdot \!\left(c\cdot \cos t-{\dfrac {a\cdot b\cdot \sin t}{\sqrt {a^{2}+b^{2}+c^{2}}}}\right)\!,\\[10pt]y=y_{0}+{\dfrac {R\cdot {\sqrt {a^{2}+c^{2}}}}{\sqrt {a^{2}+b^{2}+c^{2}}}}\cdot \sin t,\\[10pt]z=z_{0}-{\dfrac {R}{\sqrt {a^{2}+c^{2}}}}\cdot \!\left(a\cdot \cos t+{\dfrac {b\cdot c\cdot \sin t}{\sqrt {a^{2}+b^{2}+c^{2}}}}\right)\!,\end{cases}}t\in [0;2\pi ).}

Касательные и нормали[править | править код]

Уравнение касательной к окружности в точке (x1,y1){\displaystyle \left(x_{1},y_{1}\right)} определяется уравнением

(A2+x1)x+(B2+y1)y+(A2x1+B2y1+C)=0.{\displaystyle \left({\frac {A}{2}}+x_{1}\right)x+\left({\frac {B}{2}}+y_{1}\right)y+\left({\frac {A}{2}}x_{1}+{\frac {B}{2}}y_{1}+C\right)=0.}

Уравнение нормали в той же точке можно записать как

x−x12x1+A=y−y12y1+B.{\displaystyle {\frac {x-x_{1}}{2x_{1}+A}}={\frac {y-y_{1}}{2y_{1}+B}}.}

Концентрические и ортогональные окружности[править | править код]

Концентрические окружности

Окружности с общим центром, но разными радиусами, называются концентрическими. Две окружности, заданные уравнениями:

x2+y2+A1x+B1y+C1=0,x2+y2+A2x+B2y+C2=0{\displaystyle x^{2}+y^{2}+A_{1}x+B_{1}y+C_{1}=0,\;\;\;x^{2}+y^{2}+A_{2}x+B_{2}y+C_{2}=0}

являются концентрическими в том и только в том случае, когда A1=A2{\displaystyle A_{1}=A_{2}} и B1=B2.{\displaystyle B_{1}=B_{2}.}

Две окружности являются ортогональными (то есть пересекающиеся под прямым углом) тогда и только тогда, когда выполняется условие

A1A2+B1B2=2(C1+C2).{\displaystyle A_{1}A_{2}+B_{1}B_{2}=2\left(C_{1}+C_{2}\right).}

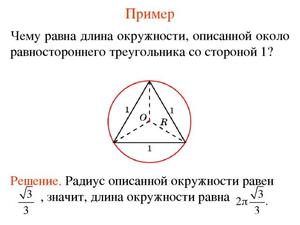
Найти длину радиуса окружности (круга), все основные формулы.

Радиус окружности — отрезок, соединяющий её центр и любую другую точку расположенную на линии окружности.
Окружность это замкнутая кривая линия, все точки которой, равноудалены от другой, определенной точки (центр окружности) на заданном расстоянии (радиус).

---

R — радиус окружности (круга)

D — диаметр, D = 2R

O — центр круга

π ≈ 3.14

 

Формула для определения длины радиуса, если известна площадь круга :

 

 

Формула для определения длины радиуса, если известна длина окружности :

 

R — радиус окружности (круга)

h — высота сегмента

L — длина хорды

O — центр круга

α — центральный угол

 

Формула для определения длины радиуса, если известна длина хорды :

 

Подробности

Автор: Сергей Кондратов

Опубликовано: 07 сентября 2011

Обновлено: 08 ноября 2017

Как рассчитать длину окружности по формулам через диаметр, равный двум радиусам

Окружность состоит из множества точек, которые находятся на равном расстоянии от центра. Это плоская геометрическая фигура, и найти ее длину не составит труда. С окружностью и кругом человек сталкивается ежедневно независимо от того, в какой сфере он работает. Многие овощи и фрукты, устройства и механизмы, посуда и мебель имеют круглую форму. Кругом называют то множество точек, которое находится в границах окружности. Поэтому длина фигуры равна периметру круга.

…

Вконтакте

Facebook

Twitter

Google+

Мой мир

Характеристики фигуры

Кроме того, что описание понятия окружности достаточно простое, её характеристики также несложные для понимания. С их помощью можно вычислить её длину. Внутренняя часть окружности состоит из множества точек, среди которых две — А и В — можно увидеть под прямым углом. Этот отрезок называют диаметром, он состоит из двух радиусов.

Это интересно: как переводить градусы в радианы?

В пределах окружности имеются точки Х такие, что не изменяется и не равняется единице отношение АХ/ВХ. В окружности это условие обязательно соблюдается, в ином случае эта фигура не имеет форму круга. На каждую точку, из которых состоит фигура, распространяется правило: сумма квадратов расстояний от этих точек до двух других всегда превышает половину длины отрезка между ними.

Основные термины окружности

Для того чтобы уметь находить длину фигуры, необходимо знать основные термины, касающиеся её. Основные параметры фигуры — это диаметр, радиус и хорда. Радиусом называют отрезок, соединяющий центр круга с любой точкой на её кривой. Величина хорды равна расстоянию между двумя точками на кривой фигуры. Диаметр — расстояние между точками, проходящее через центр фигуры.

Это интересно: какой четырёхугольник называется квадратом?

Основные формулы для вычислений

Параметры используются в формулах вычислений величин окружности:

• длину фигуры вычисляют умножением диаметра на число π и записывают таким образом: C = π*D.
• Величина диаметра в два раза превышает длину радиуса. Иной способ вычисления радиуса — необходимо разделить длину круга на удвоенное π: R = C/(2* π) = D/2.
• Диаметр рассчитывается с помощью радиуса или делением длины окружности на число π. Формула нахождения диаметра: D = C/π = 2*R.
• Площадь круга, ограниченного окружностью, можно найти двумя способами: через радиус или диаметр. По формуле площадь равна четвёртой части произведения числа π и диаметра в квадрате или радиусу в квадрате, умноженному на π: S = π*R2 = π*D2/4.

Это интересно: что такое горизонтально, что означает слово горизонталь?

Диаметр в формулах вычисления

В экономике и математике нередко появляется необходимость поиска длины окружности. Но и в повседневной жизни можно столкнуться с этой надобностью, к примеру, во время постройки забора вокруг бассейна круглой формы. Как рассчитать длину окружности по диаметру? В этом случае используют формулу C = π*D, где С — это искомая величина, D — диаметр.

Например, ширина бассейна равна 30 метрам, а столбики забора планируют поставить на расстоянии десяти метров от него. В этом случае формула расчёта диаметра: 30+10*2 = 50 метров. Искомая величина (в этом примере — длина забора): 3,14*50 = 157 метров. Если столбики забора будут стоять на расстоянии трёх метров друг от друга, то всего их понадобится 52.

Расчёты по радиусу

Как вычислить длину окружности по известному радиусу? Для этого используется формула C = 2*π*r, где С — длина, r — радиус. Радиус в круге меньше диаметра в два раза, и это правило может пригодиться в повседневной жизни. К примеру, в случае приготовления пирога в раздвижной форме.

Для того чтобы кулинарное изделие не испачкалось, необходимо использовать декоративную обёртку. А как вырезать бумажный круг подходящего размера?

Те, кто немного знаком с математикой, понимают, что в этом случае нужно умножить число π на удвоенный радиус используемой формы. Например, диаметр формы равен 20 сантиметрам, соответственно, её радиус составляет 10 сантиметров. По этим параметрам находится необходимый размер круга: 2*10*3, 14 = 62,8 сантиметра.

Это интересно: формулировка и доказательство признаков параллелограмма.

Подручные способы вычисления

Если найти длину окружности по формуле нет возможности, то стоит воспользоваться подручными методами расчёта этой величины:

• При небольших размерах круглого предмета его длину можно найти с помощью верёвки, обёрнутой вокруг один раз.
• Величину большого предмета измеряют так: на ровной плоскости раскладывают верёвку, и по ней прокатывают круг один раз.
• Современные студенты и школьники для расчётов используют калькуляторы. В режиме онлайн по известным параметрам можно узнавать неизвестные величины.

Круглые предметы в истории человеческой жизни

Первое изделие круглой формы, которое изобрёл человек — это колесо. Первые конструкции представляли собой небольшие округлые бревна, насаженные на оси. Затем появились колёса, сделанные из деревянных спиц и обода. Постепенно в изделие добавляли металлические детали для уменьшения износа. Именно для того, чтобы узнать длину металлических полос для обивки колёса, учёные прошлых веков искали формулу расчёта этой величины.

Форму колеса имеет гончарный круг, большинство деталей в сложных механизмах, конструкциях водяных мельниц и прялок. Нередко встречаются круглые предметы в строительстве — рамки круглых окон в романском архитектурном стиле, иллюминаторы в суднах. Архитекторы, инженеры, учёные, механики и проектировщики ежедневно в сфере своей профессиональной деятельности сталкиваются с надобностью расчёта размеров окружности.

Формула площади круга через диаметр или радиус или длину окружности.

Круг это плоская фигура, все точки которой, расположены на любом расстоянии от определенной точки (центр круга) но не больше заданной длины (радиус).
Радиус круга — отрезок, соединяющий центр окружности и любую, максимально удаленную от центра точку круга.
Диаметр круга — отрезок, соединяющий две любые точки максимально удаленные от центра круга и проходящий через этот центр. Диаметр, в два раза больше радиуса

---

Зная диаметр

или радиус круга или длину окружности, можно найти его площадь.

 

r — радиус круга

D — диаметр круга

π ≈ 3.14

Формула площади круга, (S):

 

 

Решения задач

на тему: Площадь круга

 

Калькулятор для расчета площади круга через радиус

 

Калькулятор для расчета площади круга через диаметр

 

 

L — длина окружности

О — центр круга

π ≈ 3.14

Формула площади круга если известна длина окружности, (S):

 

Решения задач

на тему: Площадь круга

 

Калькулятор для расчета площади круга через длину

Подробности

Автор: Сергей Кондратов

Опубликовано: 07 сентября 2011

Обновлено: 09 ноября 2017

Быстро найти нужную формулу для расчета онлайн. Геометрия. Алгебра.

Радиус окружности — отрезок, соединяющий её центр и любую другую точку расположенную на линии окружности.
Окружность это замкнутая кривая линия, все точки которой, равноудалены от другой, определенной точки (центр окружности) на заданном расстоянии (радиус).

---

R — радиус окружности (круга)

D — диаметр, D = 2R

O — центр круга

π ≈ 3.14

 

Формула для определения длины радиуса, если известна площадь круга :

 

 

Формула для определения длины радиуса, если известна длина окружности :

 

R — радиус окружности (круга)

h — высота сегмента

L — длина хорды

O — центр круга

α — центральный угол

 

Формула для определения длины радиуса, если известна длина хорды :

 

---

Сегмент — часть круга ABC, отсеченная хордой AC

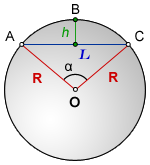
h —  высота сегмента ABC

L — хорда AC

R — радиус кружности

O — центр окружности

α — центральный угол AOC

 

Формула высоты через радиус и центральный угол, (h):

 

 

Формула высоты через хорду и центральный угол, (h):

 

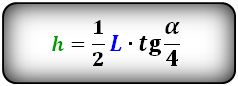
Формула высоты через радиус и хорду, (h):

---

---

 

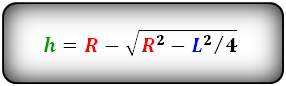
Дополнительные формулы для окружности:

---

Хорда — отрезок соединяющий любые две точки окружности. Диаметр окружности, самая большая хорда.

 

L — хорда

R — радиус окружности

O — центр окружности

α — центральный угол

 

Формула длины хорды, (L):

 

 

Калькулятор для расчета длины хорды окружности :

 

Дополнительные формулы для окружности:

Онлайн калькулятор: Сегмент круга

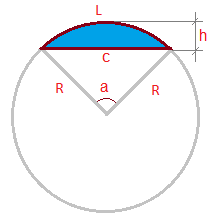Сегмент круга

Круговой сегмент — часть круга ограниченная дугой и секущей (хордой).

На рисунке:
L — длина дуги сегмента
c — хорда
R — радиус
a — угол сегмента
h — высота

Первый калькулятор рассчитывает параметры сегмента, если известен радиус и угол по следующим формулам:

Формулы вычисления параметров сегмента

Площадь сегмента:
[1]
Длина дуги:

Длина хорды:

Высота сегмента:

Сегмент

Угол в градусах, образуемый радиусами сектора

Точность вычисления

Знаков после запятой: 2

save Сохранить share Поделиться extension Виджет

Однако, как справедливо заметил наш пользователь:«на практике часто случается, что как радиус дуги, так и угол неизвестны» (см. длина дуги ). Для этого случая для расчета площади сегмента и длины дуги можно использовать следующий калькулятор:

Параметры сегмента по хорде и высоте

Точность вычисления

Знаков после запятой: 2

Угол (градусы)

 

save Сохранить share Поделиться extension Виджет

Калькулятор вычисляет радиус круга по длине хорды и высоте сегмента по следующей формуле:

Далее, зная радиус и длину хорды, легко найти угол сегмента по формуле:

Остальные параметры сегмента вычисляются аналогично первому калькулятору, по формулам, приведенным в начале статьи.

Следующий калькулятор вычисляет площадь сегмента по высоте и радиусу:

Площадь сегмента круга по радиусу и высоте

Точность вычисления

Знаков после запятой: 2

Угол (градусы)