Формула Дарси — Вейсбаха — Википедия
Формула Вейсбаха’[1] в гидравлике — эмпирическая формула, определяющая потери напора или потери давления при развитом турбулентном течении несжимаемой жидкости на гидравлических сопротивлениях (предложена Юлиусом Вейсбахом в 1855 году):
- Δh=ξ⋅V22g,{\displaystyle \Delta h=\xi \cdot {\frac {V^{2}}{2g}},}
где
Формула Вейсбаха, определяющая потери давления на гидравлических сопротивлениях, имеет вид:
- ΔP=ξ⋅V22⋅ρ,{\displaystyle \Delta P=\xi \cdot {\frac {V^{2}}{2}}\cdot \rho ,}
где
- ΔP{\displaystyle \Delta P} — потери давления на гидравлическом сопротивлении;
- ρ{\displaystyle \rho } — плотность жидкости.
Если гидравлическое сопротивление представляет собой участок трубы длиной L{\displaystyle L} и диаметром D{\displaystyle D}, то коэффициент Дарси определяется следующим образом:
- ξ=λ⋅LD,{\displaystyle \xi =\lambda \cdot {\frac {L}{D}},}
где λ{\displaystyle \lambda } — коэффициент потерь на трение по длине.
Тогда формула Вейсбаха приобретает вид:
- Δh=λ⋅LD⋅V22g,{\displaystyle \Delta h=\lambda \cdot {\frac {L}{D}}\cdot {\frac {V^{2}}{2g}},}
или для потери давления:
- ΔP=λ⋅LD⋅V22⋅ρ.{\displaystyle \Delta P=\lambda \cdot {\frac {L}{D}}\cdot {\frac {V^{2}}{2}}\cdot \rho .}
Последние две зависимости получили название формулы Дарси — Вейсбаха[2]. Предложена Ю. Вейсбахом (L. J. Weisbach, 1845) и А. Дарси (1857).
Если определяются потери на трение по длине для трубы некруглого поперечного сечения, то D{\displaystyle D} представляет собой гидравлический диаметр.
Следует отметить, что потери напора на гидравлических сопротивлениях не всегда пропорциональны скоростному напору.
Определение коэффициента потерь на трение по длине[править | править код]
Коэффициент λ{\displaystyle \lambda } определяется по-разному для разных случаев.
Для ламинарного течения в гладких трубах с жёсткими стенками, коэффициент потерь на трение по длине определяется по формуле Пуазейля:
- λ=64Re,{\displaystyle \lambda ={\frac {64}{\mathrm {Re} }},}
где Re{\displaystyle \mathrm {Re} } — число Рейнольдса.
Иногда для гибких труб в расчётах принимают
- λ=68Re.{\displaystyle \lambda ={\frac {68}{\mathrm {Re} }}.}
Для турбулентного течения существуют более сложные зависимости. Одна из наиболее часто используемых формул — это формула Блазиуса:
- λ=0,316Re4.{\displaystyle \lambda ={\frac {0,316}{\sqrt[{4}]{\mathrm {Re} }}}.}
Эта формула даёт хорошие результаты при числах Рейнольдса, изменяющихся в пределах от критического числа Рейнольдса Reкр{\displaystyle \mathrm {Re_{\text{кр}}} } до значений Re=105{\displaystyle \mathrm {Re} =10^{5}}. Формула Блазиуса применяется для гидравлически гладких труб.
Для значений Re=105−106{\displaystyle \mathrm {Re} =10^{5}-10^{6}} применяют формулу Никурадзе: λ=0,0032+0,221/Re0,237.{\textstyle \lambda =0,0032+0,221/Re^{0,237}.}[3] Также, применяются формулы Женеро, Альтшуля, Канакова и других.
Для значений Рейнольдса больше 104{\displaystyle 10^{4}} применяется формула Горшкова-Кантакузена, полученная методом регрессионного анализа[4]: λ=0,2579Re0,231.{\displaystyle \lambda ={\frac {0,2579}{\mathrm {Re^{0,231}} }}.} Тем же автором была выведена формула для вычисления критерия Рейнольдса в гемодинамике (течении крови).[5]
Для гидравлически шероховатых труб коэффициент потерь на трение по длине определяется графически по эмпирическим зависимостям. Графики для определения коэффициента потерь на трение по длине для шероховатых труб можно посмотреть здесь (k — размер шероховатости, d — диаметр трубы).
Определение коэффициента Дарси для местных сопротивлений[править | править код]
Рис. 1. Гидравлический конфузор: Q1{\displaystyle Q_{1}} — поток жидкости в широком сечении трубы; Q2{\displaystyle Q_{2}} — поток жидкости в узком сечении трубыДля каждого вида местных сопротивлений существуют свои зависимости для определения коэффициента ξ{\displaystyle \xi }.
К числу наиболее распространённых местных сопротивлений относятся внезапное расширение трубы, внезапное сужение трубы и поворот трубы.
1. При внезапном расширении трубы:
- ξ=(1−S1S2)2,{\displaystyle \xi =\left(1-{\frac {S_{1}}{S_{2}}}\right)^{2},}
где S1{\displaystyle S_{1}} и S2{\displaystyle S_{2}} — площади поперечного сечения трубы, соответственно перед расширением и после него.
2. При внезапном сужении трубы коэффициент Дарси определяется по формуле:
Рис. 2. Зависимость коэффициента Дарси от угла δ{\displaystyle \delta } поворота трубы- ξ=1−S2/S12,{\displaystyle \xi ={\frac {1-S_{2}/S_{1}}{2}},}
где S1{\displaystyle S_{1}} и S2{\displaystyle S_{2}} — площади поперечного сечения трубы, соответственно, перед сужением и после него.
3. При постепенном сужении трубы (конфузор):
- ξ=λT8sinα/2(1−1n2),{\displaystyle \xi ={\frac {\lambda _{T}}{8\sin {\alpha /2}}}\left(1-{\frac {1}{n^{2}}}\right),}
где n=S1S2{\displaystyle n={\frac {S_{1}}{S_{2}}}} — степень сужения; λT{\displaystyle \lambda _{T}} — коэффициент потерь на трение по длине при турбулентном режиме.
4. При резком (без закругления) повороте трубы (колено) коэффициент Дарси определяется по графическим зависимостям (рис. 2).
Исторически формула Дарси — Вейсбаха была получена как вариант формулы Прони.
- ↑ Формула Вейсбаха в Физической энциклопедии
- ↑ Дарси-Вейсбаха формула в Физической энциклопедии
- ↑ М.П. Малков, И.Б. Данилов, А.Г. Зельдович, А.Б. Фрадков. Справочник по физико-техническим основам криогеники. — «Энергия», 1973. — С. 242-243. — 392 с.
- ↑ Горшков-Кантакузен В. А. К вопросу вычисления коэффициента Дарси методом регрессионного анализа // Материалы XXI Международного симпозиума «Динамические и технологические проблемы механики конструкций и сплошных сред» имени А. Г. Горшкова, 16 – 20 февраля 2015, Вятичи.. — 2015. — № Том 1. — С. 59-60. — ISSN 978-5-906099-81-5.
- ↑ Горшков-Кантакузен В.А. Вычисление критерия Рейнольдса в рамках гемодинамики // Бюллетень НЦССХ им. А.Н. Бакулева «сердечно-сосудистые заболевания» : (Приложение). — май-июнь 2015. — № 3 Т.6. — С. С. 180. — ISSN 1810-0694.
- Гидравлика, гидромашины и гидроприводы: Учебник для машиностроительных вузов/ Т. М. Башта, С. С. Руднев, Б. Б. Некрасов и др. — 2-е изд., перераб. — М.: Машиностроение, 1982.
- Гейер В. Г., Дулин В. С., Заря А. Н. Гидравлика и гидропривод: Учеб для вузов. — 3-е изд., перераб. и доп. — М.: Недра, 1991.
- Горшков-Кантакузен В. А. К вопросу вычисления коэффициента Дарси методом регрессионного анализа // Материалы XXI Международного симпозиума «Динамические и технологические проблемы механики конструкций и сплошных сред» имени А. Г. Горшкова, 16 — 20 февраля 2015, Вятичи. Том 1 / МАИ. — М.: ООО «ТРП», 2015. С. 59-60
Гидравлические потери по длине
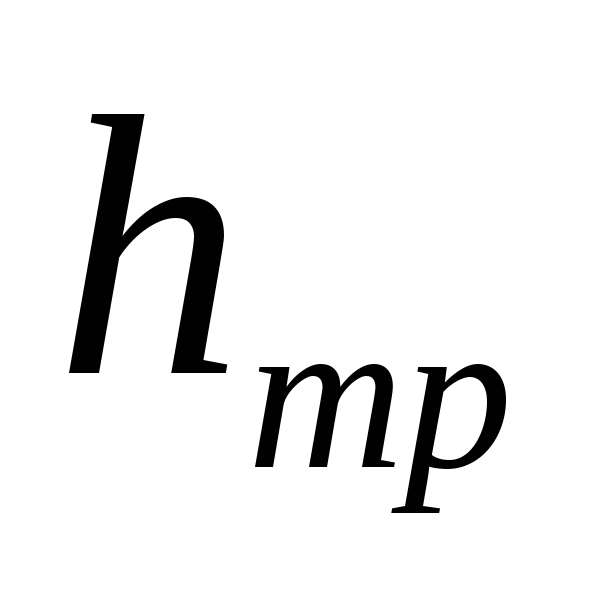 ,
в чистом виде, т.е. так, что нет никаких
других потерь, возникают в гладких
прямых трубах с постоянным сечением
при равномерном течении. Такие потери
обусловлены внутренним трением в
жидкости и поэтому происходят и в
шероховатых трубах, и в гладких. Величина
этих потерь выражается зависимостью
,
в чистом виде, т.е. так, что нет никаких
других потерь, возникают в гладких
прямых трубах с постоянным сечением
при равномерном течении. Такие потери
обусловлены внутренним трением в
жидкости и поэтому происходят и в
шероховатых трубах, и в гладких. Величина
этих потерь выражается зависимостью 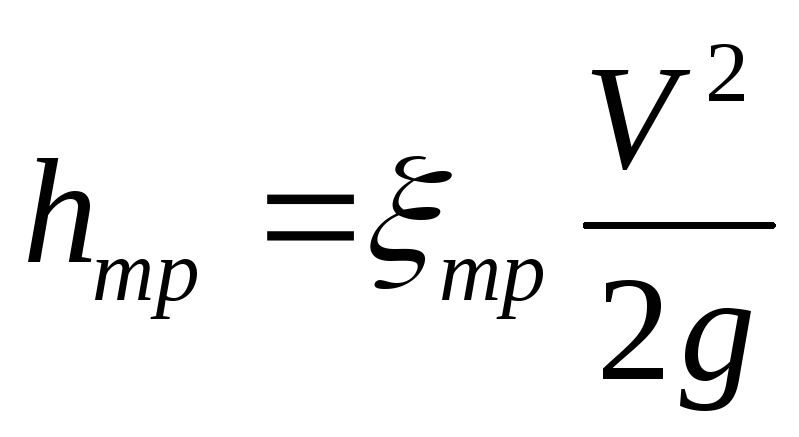 ,
,
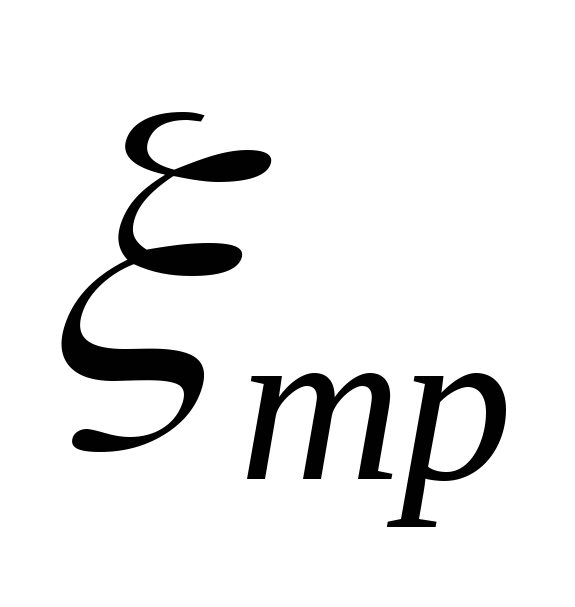 — коэффициент сопротивления, обусловленный
трением по длине.
— коэффициент сопротивления, обусловленный
трением по длине.При равномерном движении жидкости на участке трубопровода постоянного диаметра d длиной l этот коэффициент сопротивления прямо пропорционален длине и обратно пропорционален диаметру трубы
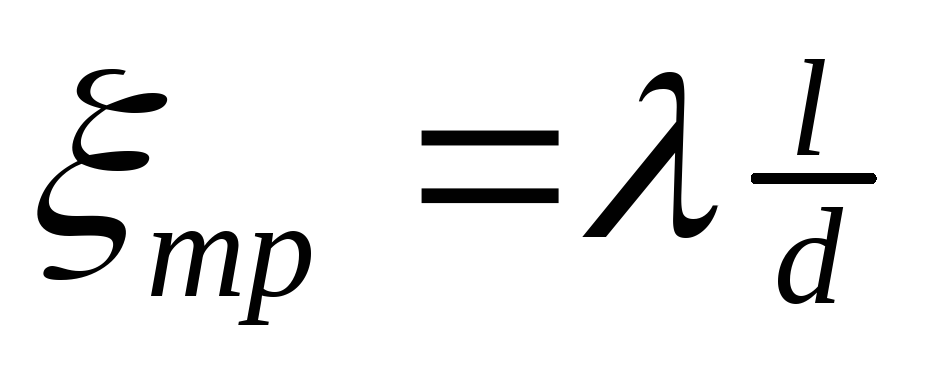 ,
,
где – коэффициент гидравлического трения (иначе его называют коэффициент потерь на трение или коэффициент сопротивления трения).
Из этого выражения нетрудно видеть, что значение — коэффициент трения участка круглой трубы, длина которого равна её диаметру.
С учетом последнего выражения для коэффициента сопротивления потери напора по длине выражаются формулой Дарси
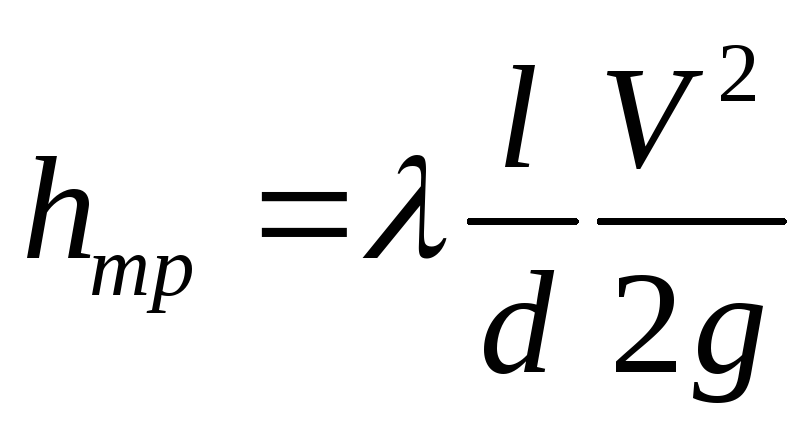 .
.
Эту формулу можно
применять не только для цилиндрических
трубопроводов, но тогда надо выразить
диаметр трубопровода d через гидравлический
радиус потока 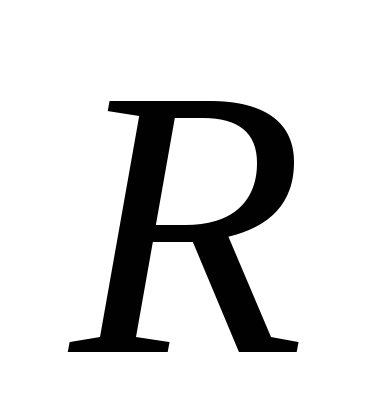
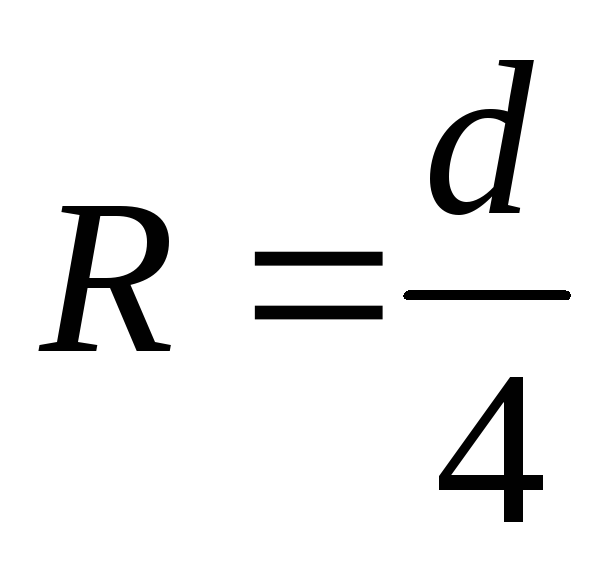 или
или 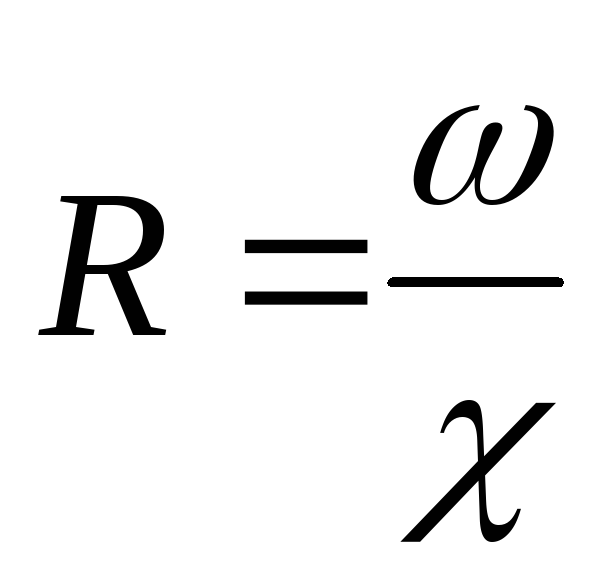
где, напомним, ω – площадь живого сечения потока,
χ — смоченный периметр.
Гидравлический радиус можно вычислить для потока с любой формой сечения, и тогда формула Дарси принимает вид
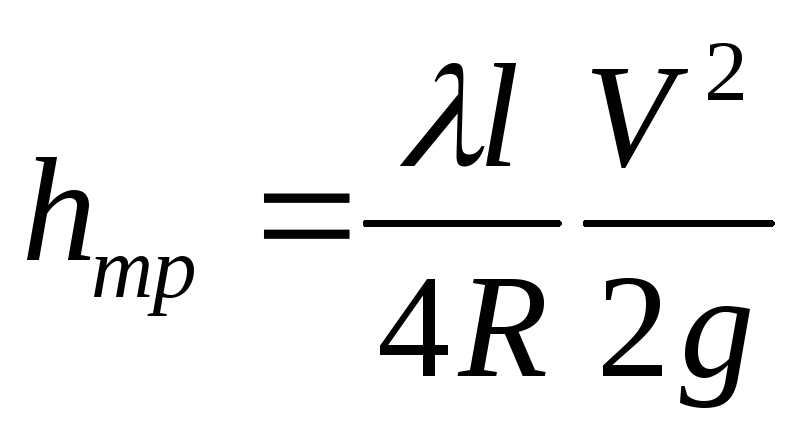 .
.
Эта формула справедлива как для ламинарного, так и для турбулентного режимов движения жидкости, однако коэффициент трения по длине
Д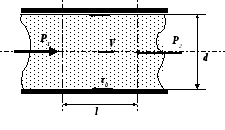 ля
определения физического смысла
коэффициентаλ рассмотрим объём жидкости длиной l,
который равномерно движется в трубе
диаметром d со скоростью V.
На этот объём действуют силы давления P1и P2,
причём P1 > P2,
и силы трения рассматриваемого объёма
о стенки трубы, которые определяются
напряжением трения на стенке трубы
ля
определения физического смысла
коэффициентаλ рассмотрим объём жидкости длиной l,
который равномерно движется в трубе
диаметром d со скоростью V.
На этот объём действуют силы давления P1и P2,
причём P1 > P2,
и силы трения рассматриваемого объёма
о стенки трубы, которые определяются
напряжением трения на стенке трубы
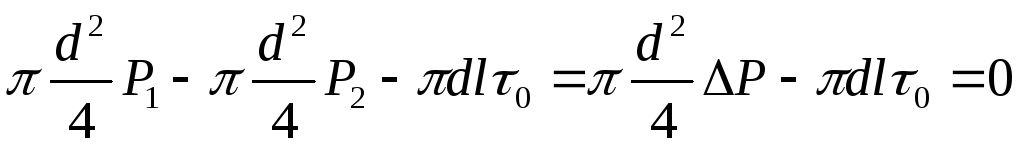 .
.
Если учесть, что
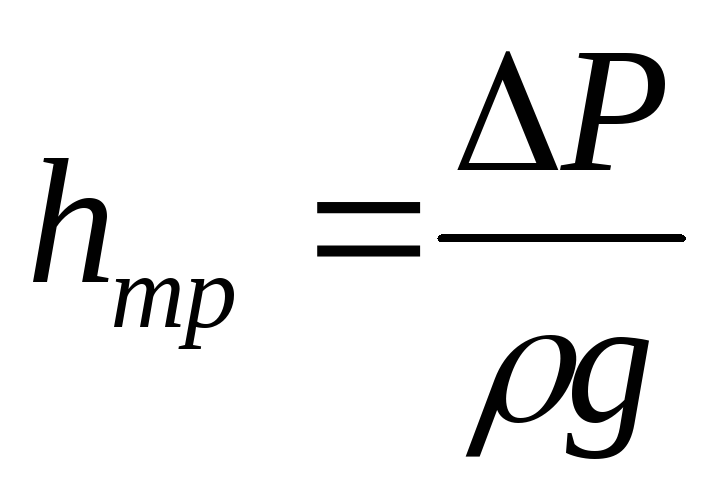 , то
, то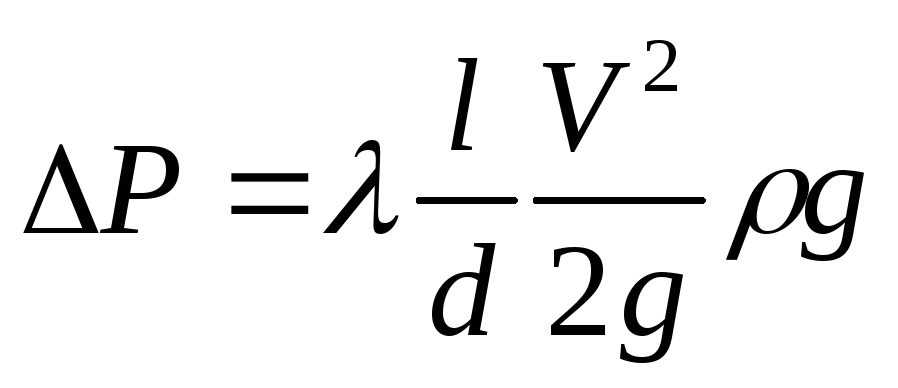 ,
,
и подставить эту величину в уравнение сил, действующих на рассматриваемый объём, получим:
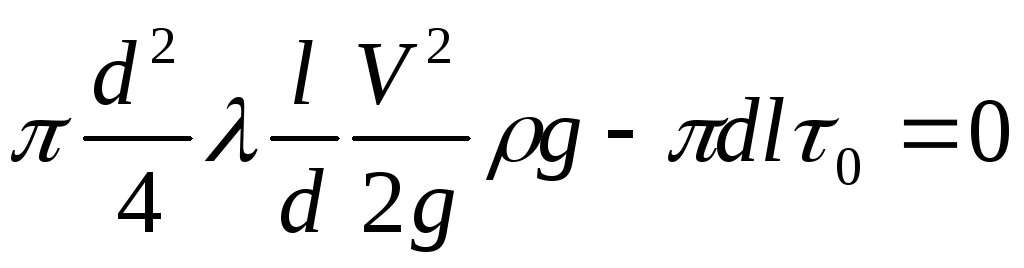
Сократив последнее
выражение, получим 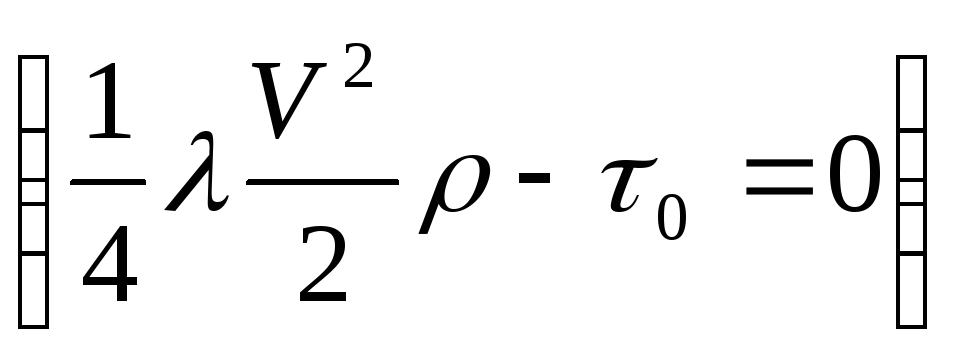 . Выразив из негоλ,
окончательно будем иметь
. Выразив из негоλ,
окончательно будем иметь
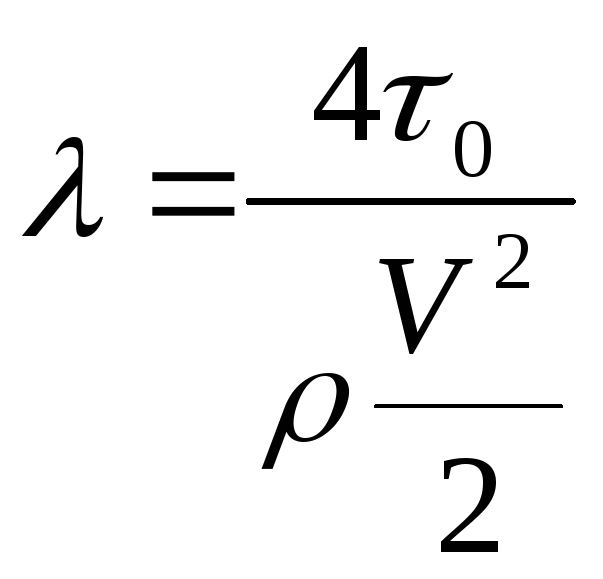 .
.
Из полученного выражения следует, что коэффициент гидравлического трения есть величина, пропорциональная отношению напряжения трения на стенке трубы к гидродинамическому давлению, посчитанному по средней скорости потока. Приведённые выше рассуждения и полученные в результате них формулы справедливы как для ламинарного, так и для турбулентного потоков. Однако коэффициент
Ламинарное течение жидкости
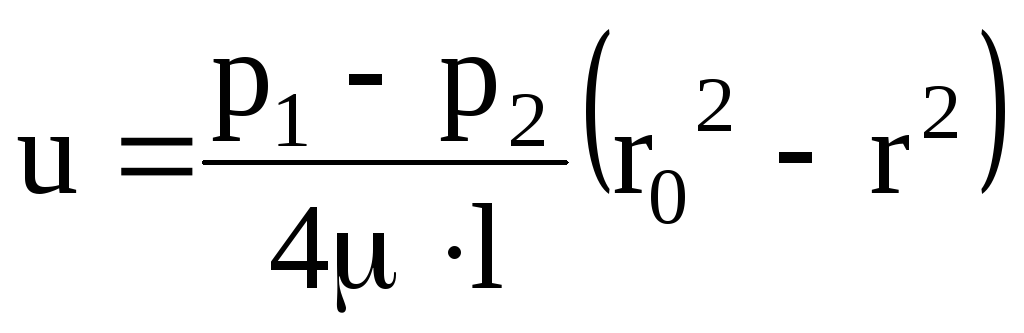
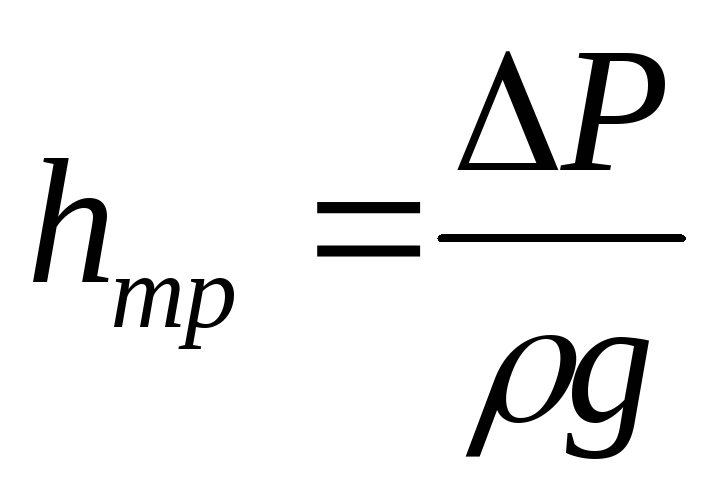

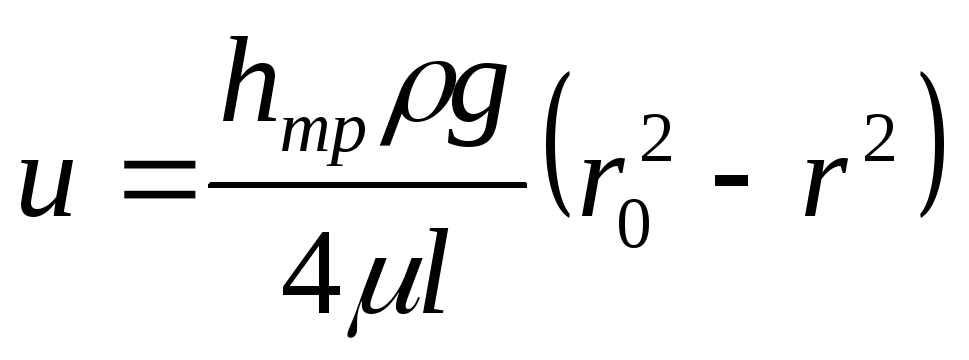
Используя значение скорости u, определим величину расхода через кольцевую площадь dωc шириной dr, находящуюся на расстоянии r от центра трубы. Выше было отмечено, что скорость в любой точке этого кольца одинакова, и тогда

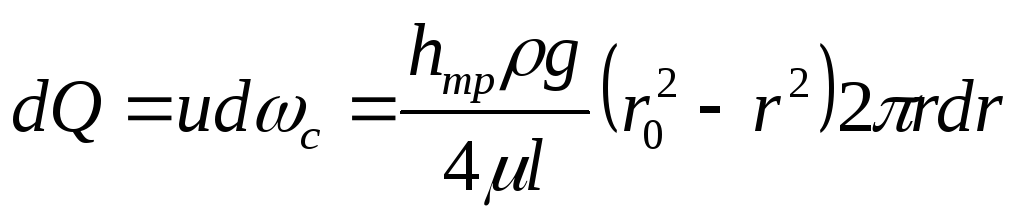 .
.
Проинтегрировав dQ по всей площади трубы (т.е. от r = 0 до r
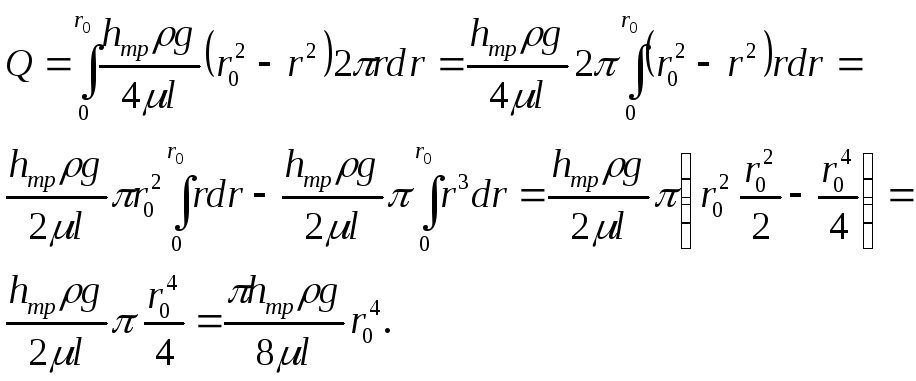
Средняя скорость в таком потоке будет
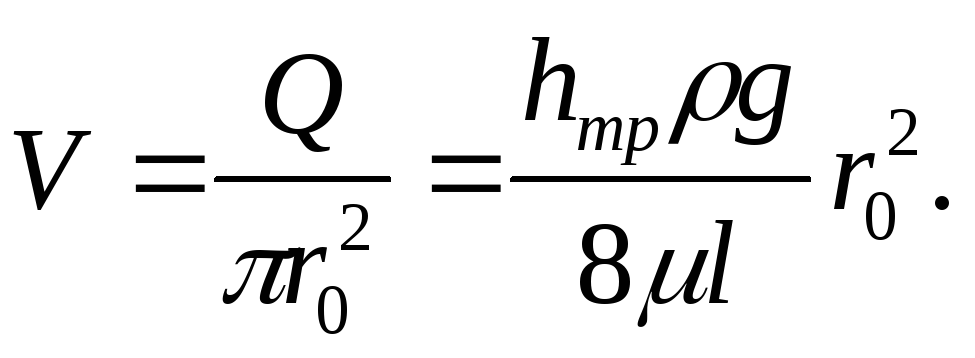
Заметим, что средняя скорость потока с параболическим распределением скоростей вдвое меньше максимальной.
Из последнего выражения легко получить закон сопротивления потоку, т.е. зависимость потерь энергии от размеров и параметров движения жидкости:
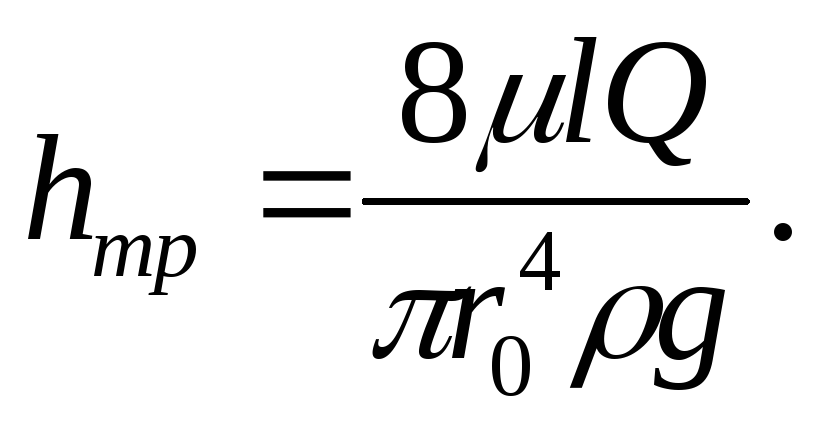
Заменив в этом
выражении динамический коэффициент
вязкости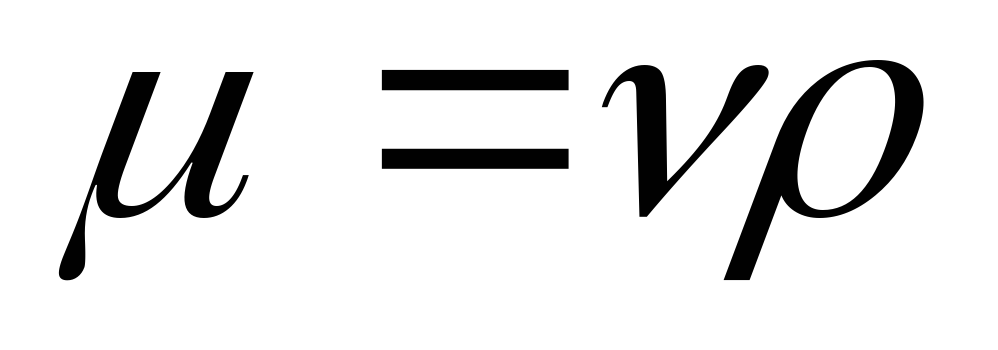 кинематическим и выразив радиус трубыr0 через диаметр d, получим
кинематическим и выразив радиус трубыr0 через диаметр d, получим
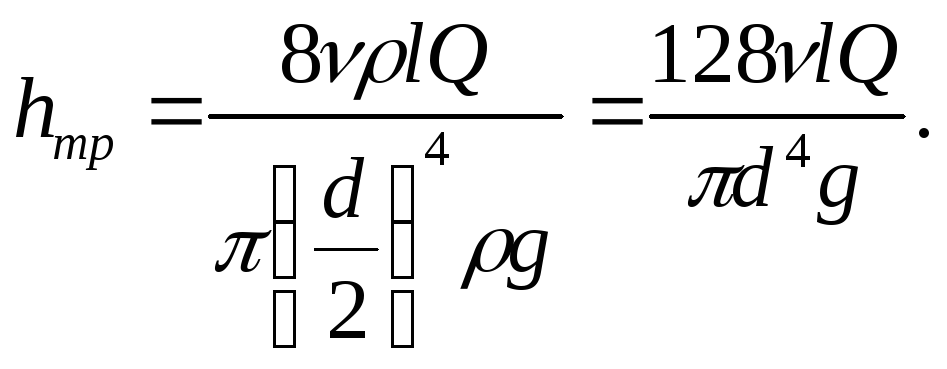
Полученное выражение носит название закона Пуазейля и применяется для расчета потерь энергии с ламинарным течением.
Эту же величину потерь на трение ранее мы выразили формулой Дарси. Если приравнять правые части формулы Дарси и закона Пуазейля, получится:
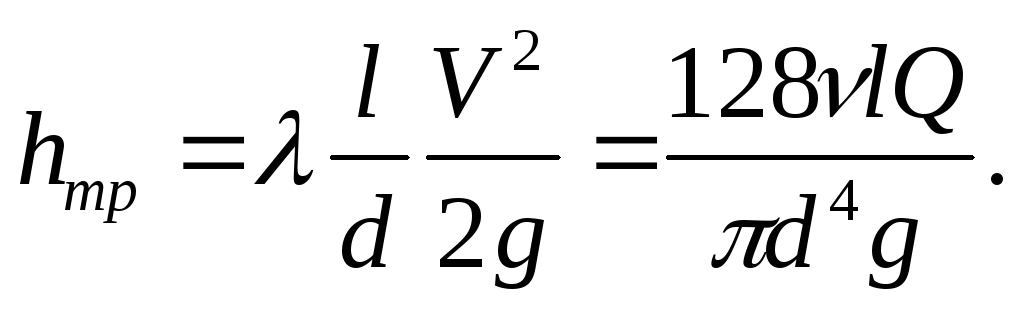
Заменим расход
произведением 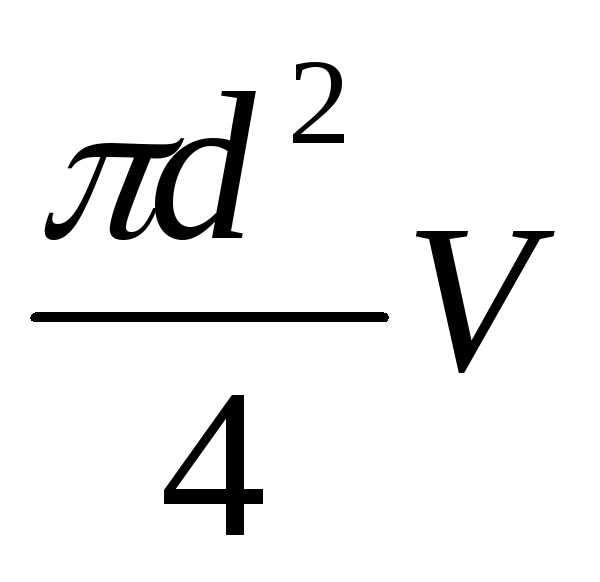 и подставим в последнее равенство
и подставим в последнее равенство
 .
.
Искусственно умножим и разделим числитель и знаменатель на V:
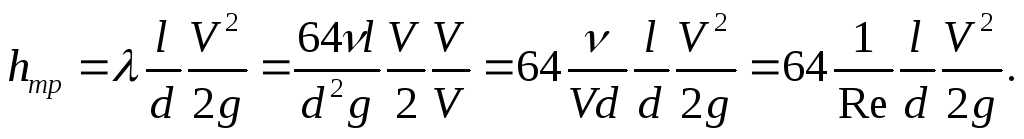
Очевидно, что в этом случае
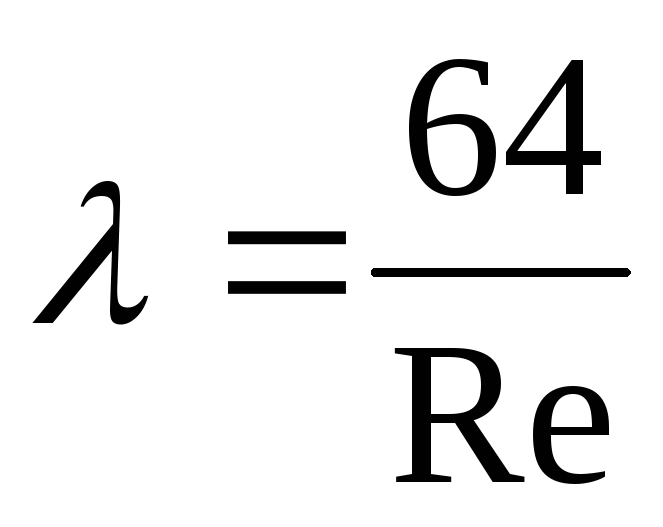 .
.
Это выражение для
коэффициента гидравлического трения
при ламинарном движении жидкости хорошо
подтверждается экспериментом и
используется на практике для определения
потерь энергии в потоке при ламинарном
течении. Иногда этот коэффициент
обозначается 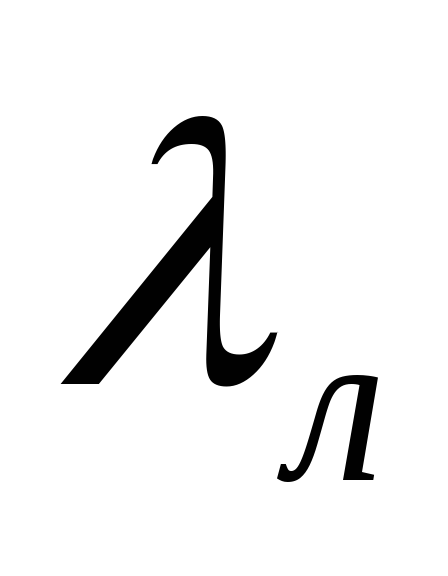 .
.
4.4. Потери напора по длине при равномерном установившемся движении жидкости
При равномерном установившемся движении жидкости в трубе средняя скорость и распределение скоростей по длине остаются неизменными. Следовательно, при определении потерь напора по длине можно использовать основное уравнение равномерного движения как при ламинарном, так и турбулентном движении в круглой трубе, выразив касательное напряжение на стенке формулой
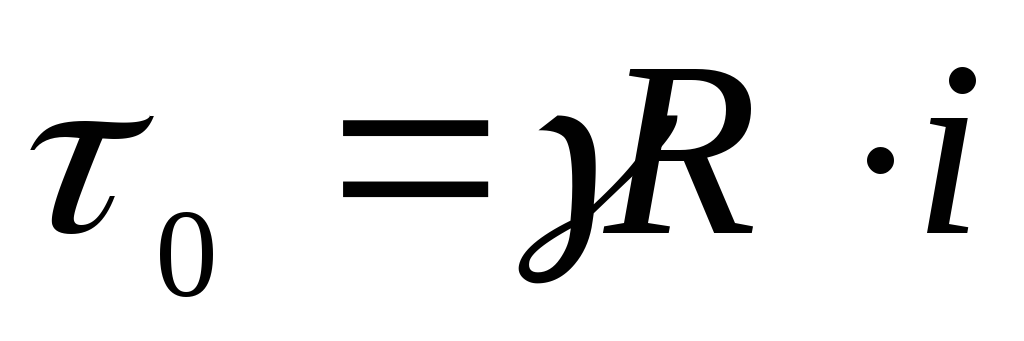 .
.
Для круглой трубы
диаметром  гидравлический
радиус
гидравлический
радиус 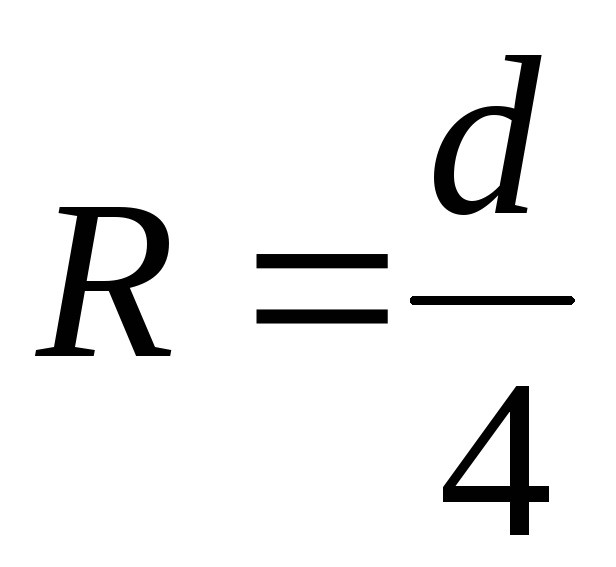 (
(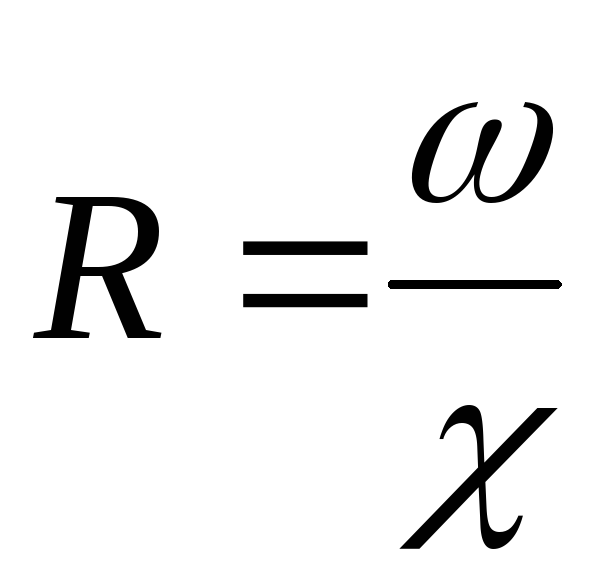 ,
площадь живого сечения
,
площадь живого сечения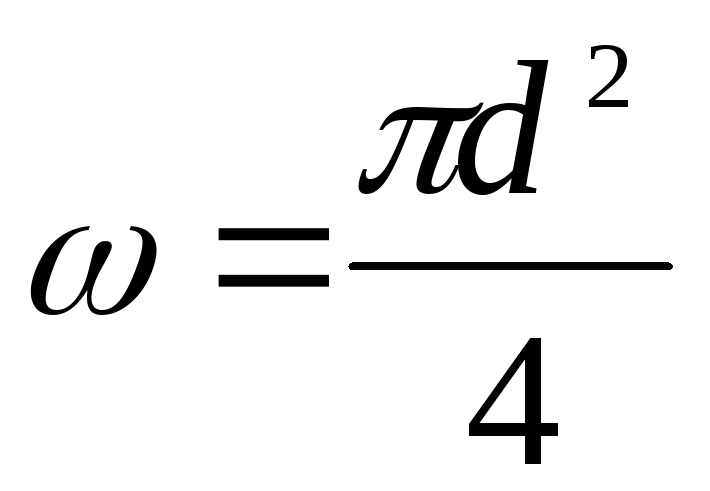 ,
смоченный периметр
,
смоченный периметр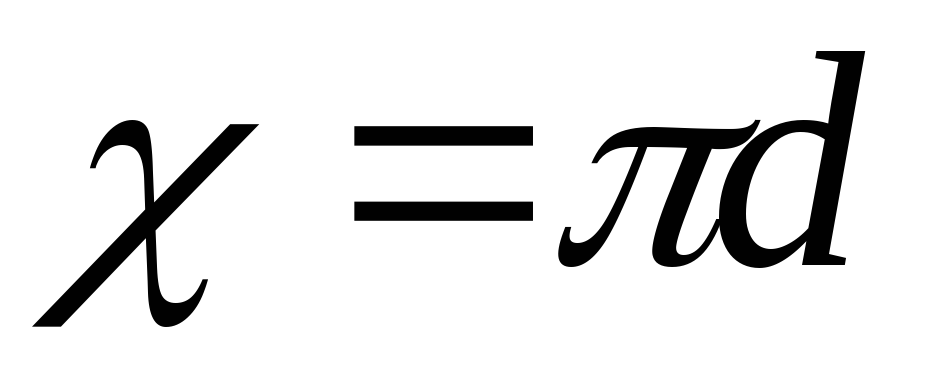 ).
Так как гидравлический уклон
).
Так как гидравлический уклон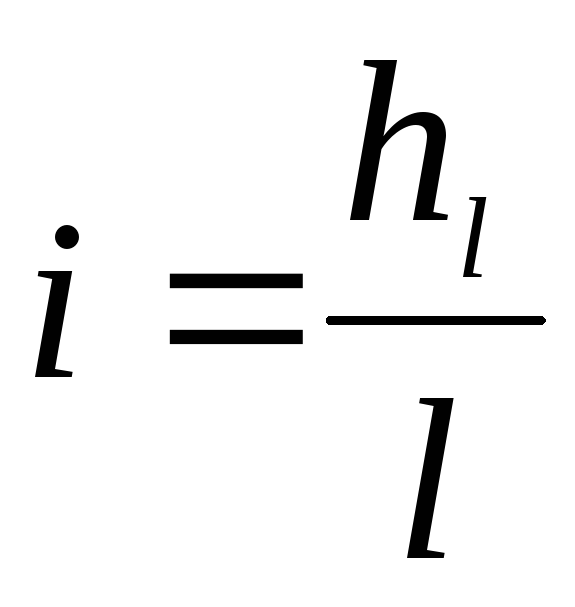 ,
то касательные напряжения на внутренней
поверхности трубы при движении вязкой
жидкости будут равны
,
то касательные напряжения на внутренней
поверхности трубы при движении вязкой
жидкости будут равны
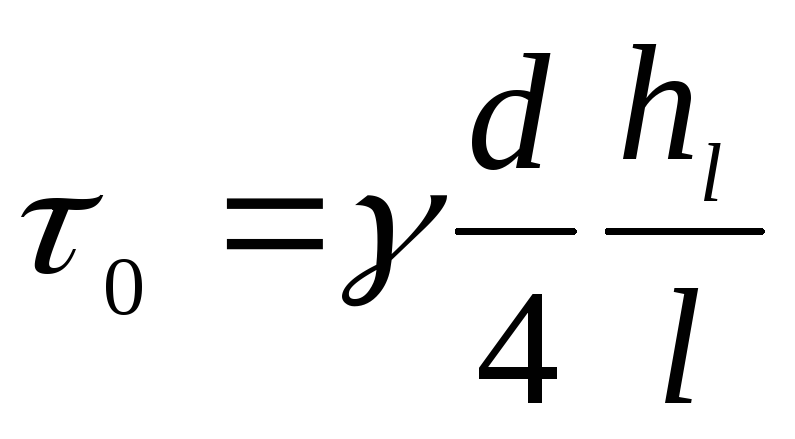 (4.25)
(4.25)
Опытами было
установлено, что сила сопротивления 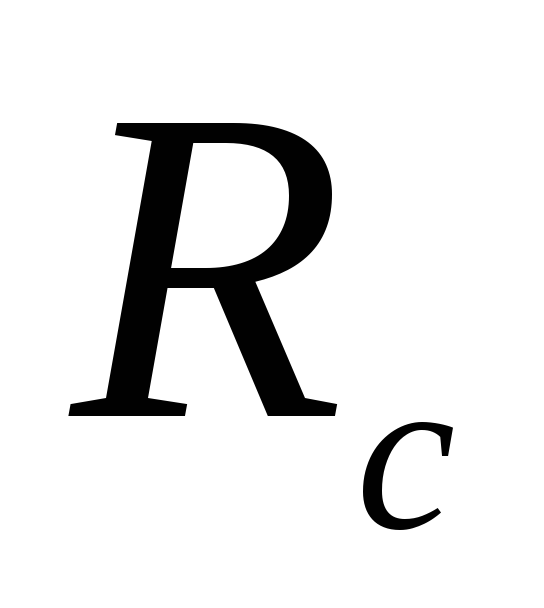 при обтекании твердого тела вязкой
жидкостью при установившемся движении
зависит от определенных параметров и
эти сопротивления можно представить в
виде следующей функциональной зависимости:
при обтекании твердого тела вязкой
жидкостью при установившемся движении
зависит от определенных параметров и
эти сопротивления можно представить в
виде следующей функциональной зависимости:
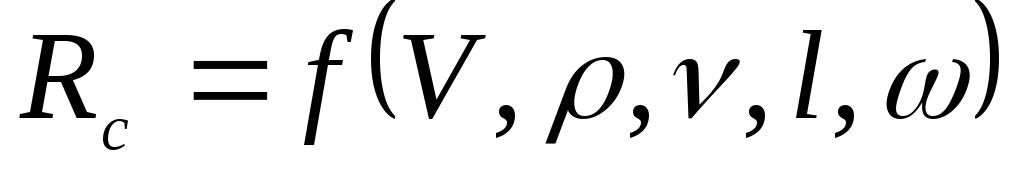 , (4.26)
, (4.26)
где V — скорость
набегающего потока жидкости;  — плотность жидкости;
— плотность жидкости;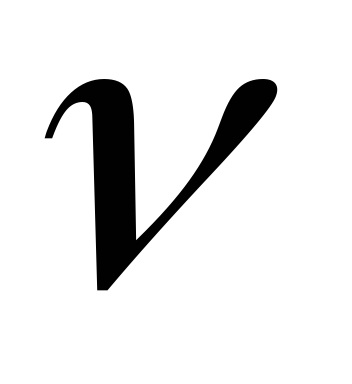 — кинематическая вязкость;
— кинематическая вязкость;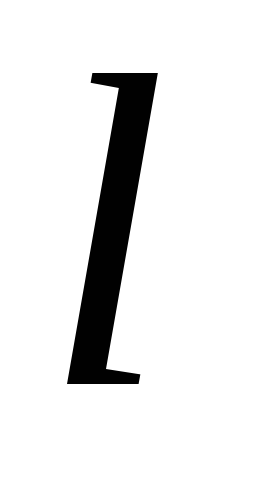 — характерный линейный размер тела;
— характерный линейный размер тела; — наибольшее сечение тела, которое
перпендикулярно вектору скорости
— наибольшее сечение тела, которое
перпендикулярно вектору скорости набегающего потока.
набегающего потока.
На основании анализов опытов и использования теории размерностей сила сопротивления может быть представлена следующей формулой:
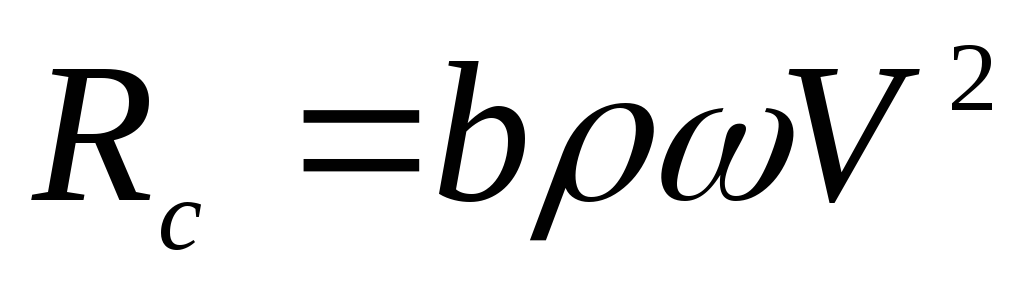 , (4.27)
, (4.27)
где b — некоторый
безразмерный коэффициент пропорциональности,
называемый коэффициентом сопротивления;  — площадь тела.
— площадь тела.
Полагаем, что касательные напряжения, возникающие на поверхности тела, равны
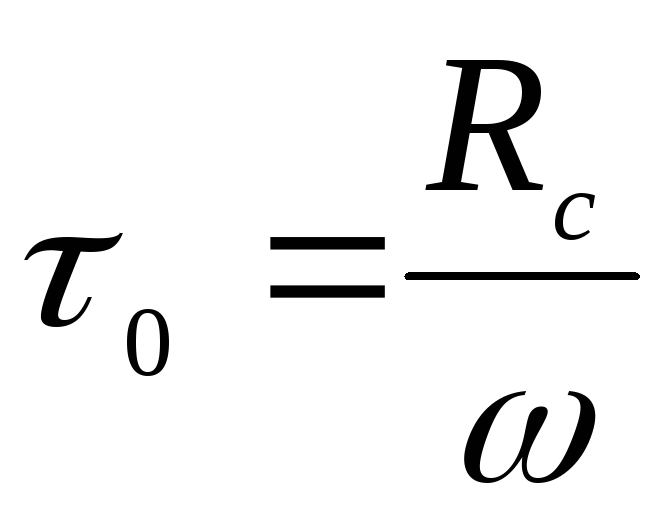 . (4.28)
. (4.28)
Тогда
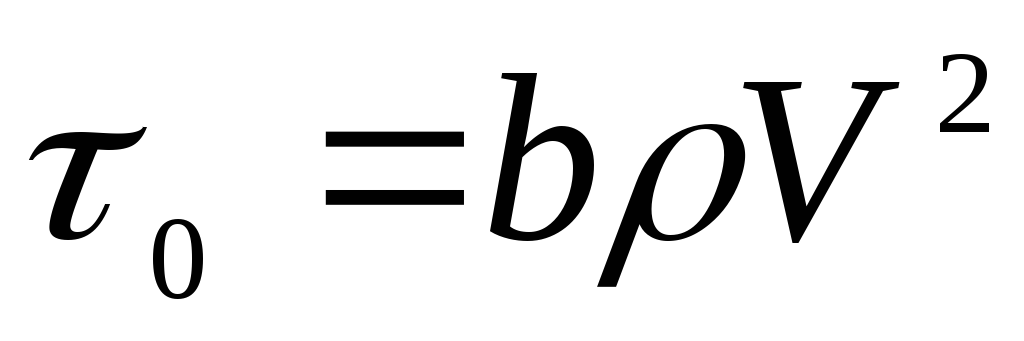 . (4.29)
. (4.29)
Воспользуемся полученной зависимостью для нахождения выражения по определению потерь напора по длине круглой трубы. Считаем, что касательные напряжения на поверхности трубы можно выразить зависимостью (4.29), V — средняя скорость в трубе.
Напишем равенство, используя формулы (4.25) и (4.29):
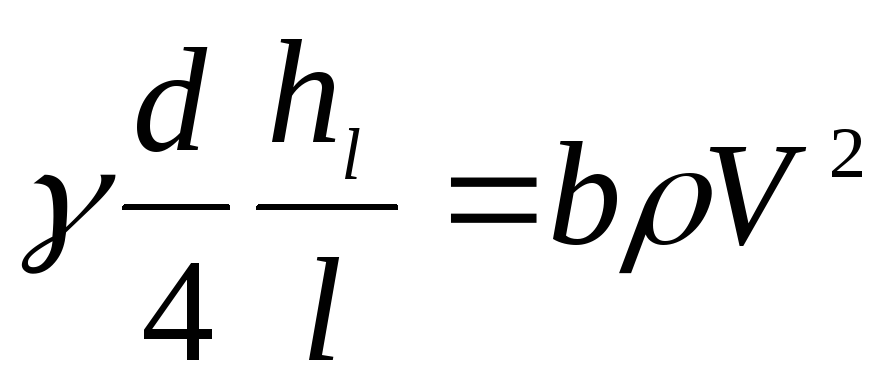 . (4.30)
. (4.30)
Потери напора по длине определим из равенства
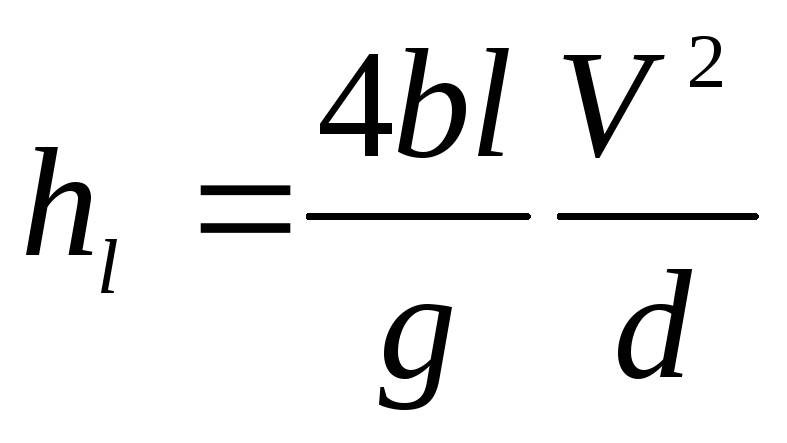 . (4.31)
. (4.31)
Умножив и разделив на 2 выражение (4.31), получим
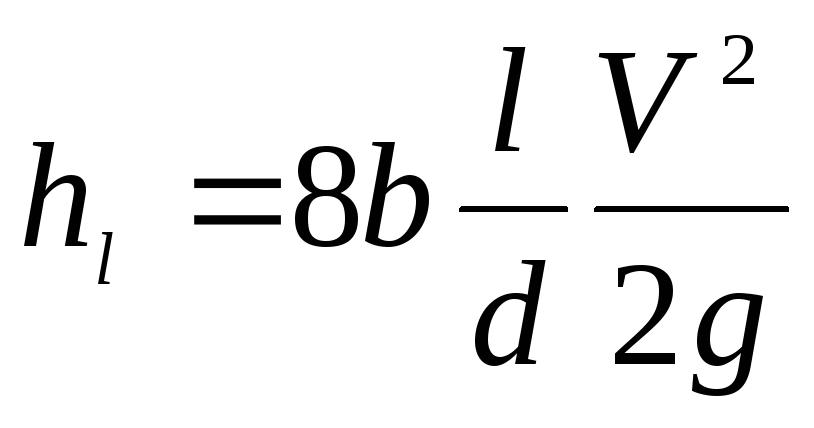 . (4.32)
. (4.32)
Обозначим 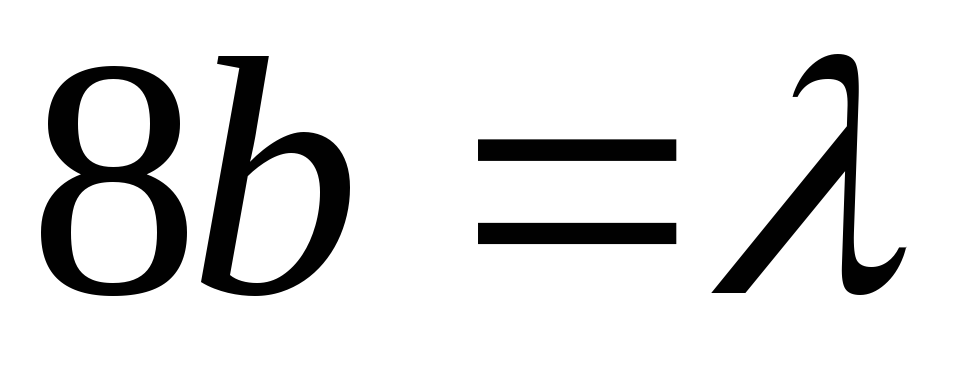 ,
, -безразмерный
коэффициент, который получил название коэффициента
гидравлического трения.
-безразмерный
коэффициент, который получил название коэффициента
гидравлического трения.
Окончательная форма потерь напора по длине имеет следующий вид:
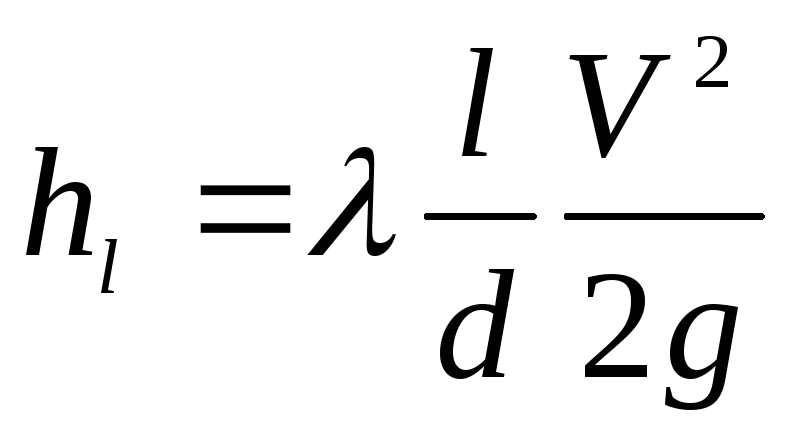 . (4.33)
. (4.33)
Формулу (4.33) принято называть формулой Вейсбаха-Дарси.
Учитывая уравнение равномерного движения в виде (4.24), коэффициент гидравлического трения можно выразить в виде
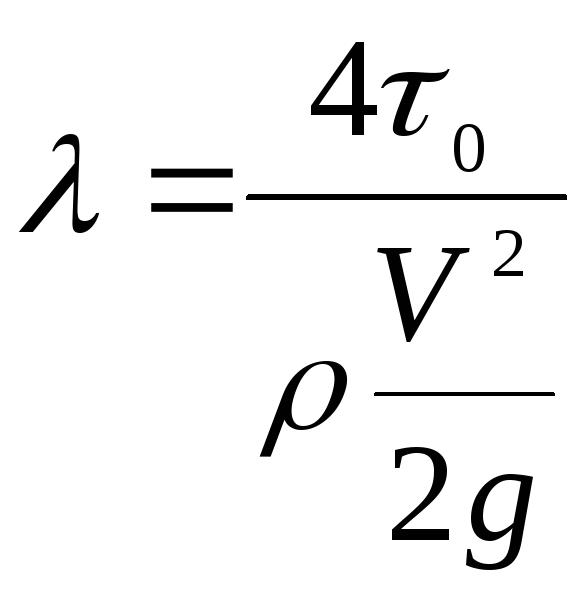 , (4-34)
, (4-34)
где 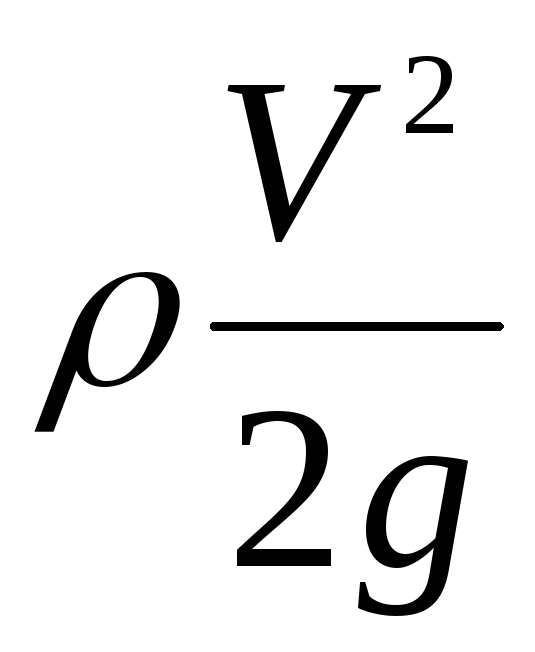 — динамическое давление.
— динамическое давление.
Коэффициент  пропорционален
отношению касательных напряжений на
стенке трубы к динамическому давлению,
создаваемому потоком жидкости. В общем
случае коэффициент гидравлического
трения
пропорционален
отношению касательных напряжений на
стенке трубы к динамическому давлению,
создаваемому потоком жидкости. В общем
случае коэффициент гидравлического
трения  зависит от
режима движения (ламинарного или
турбулентного). На касательные напряжения
на стенке
зависит от
режима движения (ламинарного или
турбулентного). На касательные напряжения
на стенке 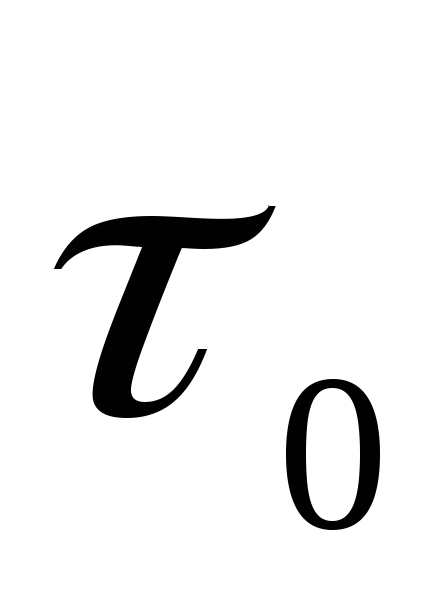 трубы влияет шероховатость ее поверхности.
трубы влияет шероховатость ее поверхности.
В случае безнапорного движения жидкости в различных руслах (каналы, канализационные и дренажные трубы) формула Вейсбаха-Дарси (4.33) не может быть применена. Для безнапорного установившегося равномерного турбулентного движения жидкости гидравлические потери по длине потока вычисляются по формуле Шези.
Для вывода формулы
Шези используем зависимости (4.23) и (4.29)
для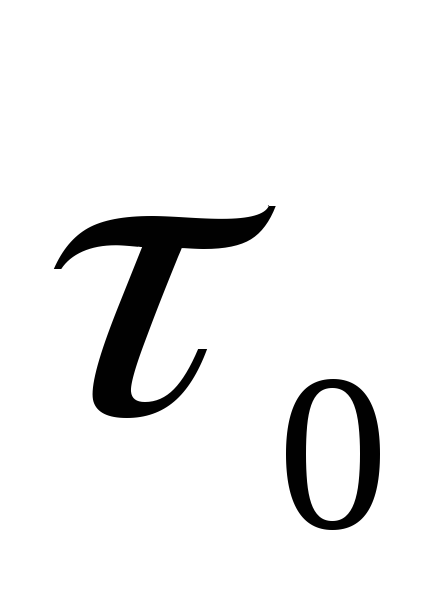 .
Напишем равенство
.
Напишем равенство
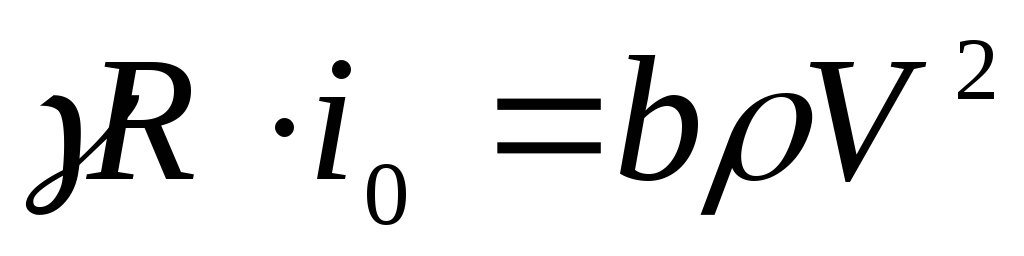 . (4.35)
. (4.35)
Средняя скорость в русле из (4.35)
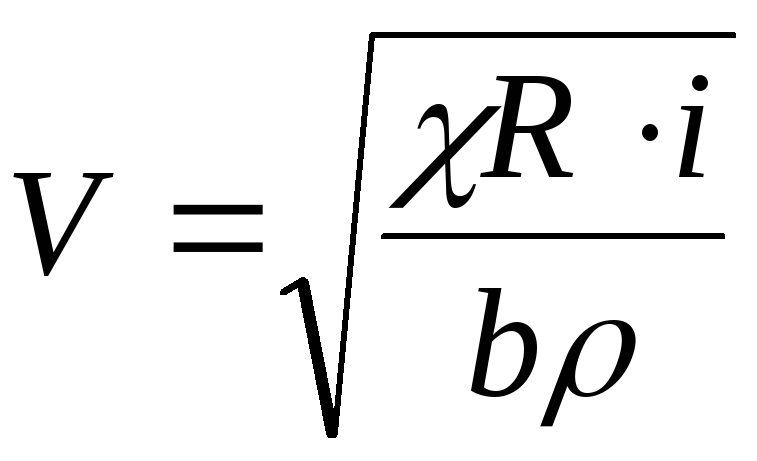 . (4.36)
. (4.36)
Или, учитывая, что 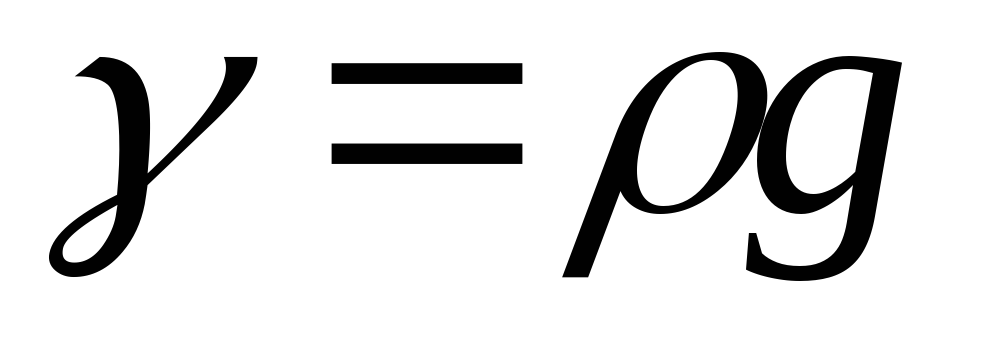 ,
,
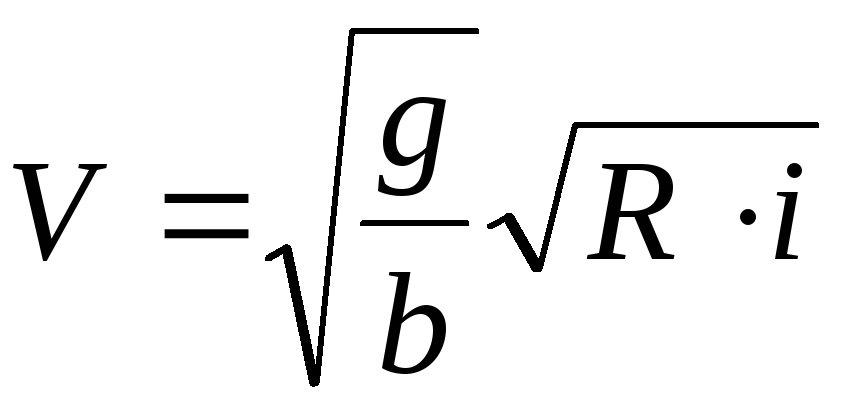 (4.37)
(4.37)
В полученной
зависимости обозначаем 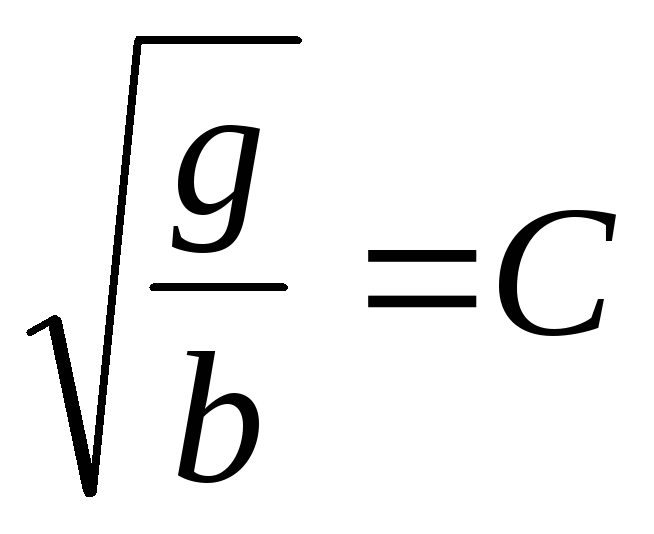 .
Коэффициент С получил название коэффициента
Шези.
.
Коэффициент С получил название коэффициента
Шези.
Средняя скорость при равномерном движении жидкости в русле
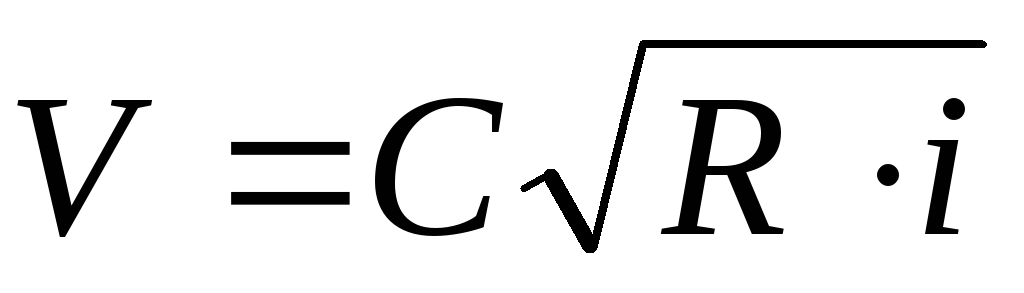 . (4.38)
. (4.38)
Расход в русле
площадью живого сечения  составляет
составляет
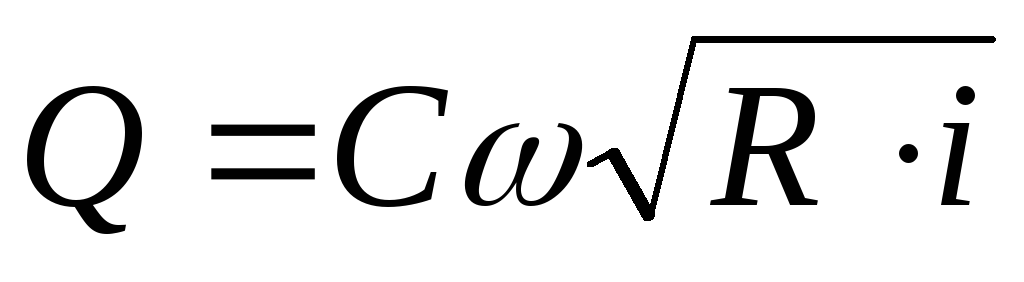 . (4.39)
. (4.39)
Зависимости (4.38) и (4.39) называют формулами Шези.
Формулы Шези могут служить для определения средней скорости в случае установившегося равномерного движения жидкости не только в безнапорных руслах, но и в трубах.
Следует учитывать, что формула применима только в случае квадратичной области сопротивления. Значения коэффициента С определяются по эмпирическим формулам, полученным в результате опытов с открытыми руслами и трубами.
Для удобства использования формул Шези вводят следующие обозначения:
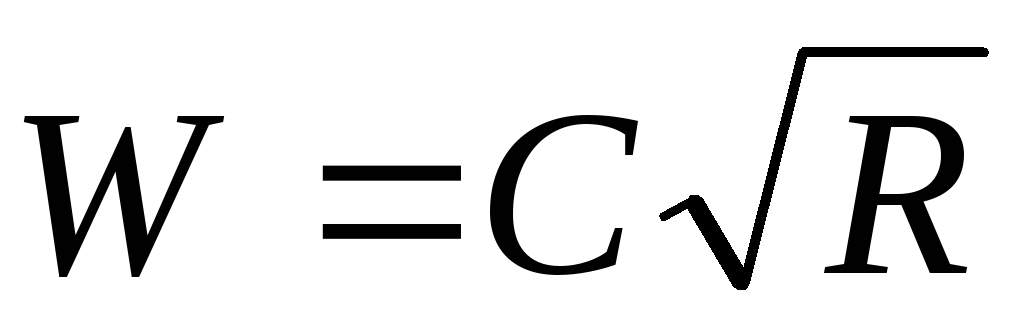 — модуль
скорости, м/с;
— модуль
скорости, м/с;
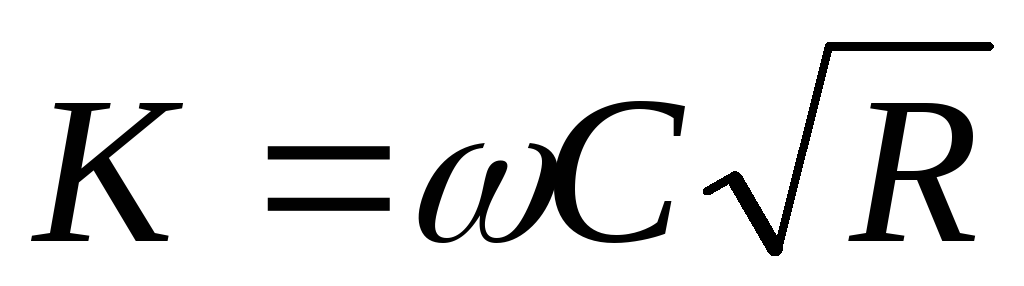 — модуль расхода,
м/с. (4.40)
— модуль расхода,
м/с. (4.40)
С учетом выражений модулей скорости и расхода формулы Шези принимают вид:
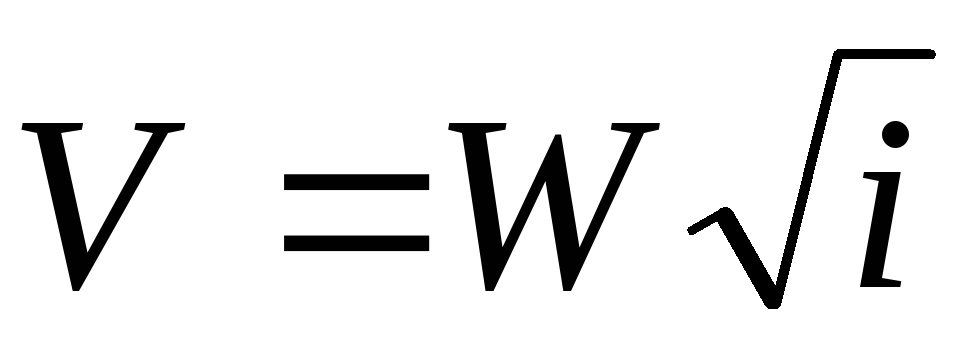 ;
;
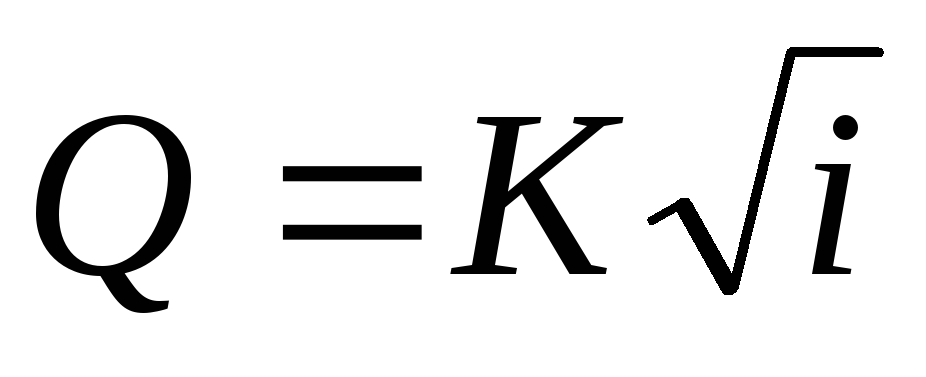 .(4.41)
.(4.41)
Гидравлические
потери напора по длине трубы получим
из формулы Шези, где 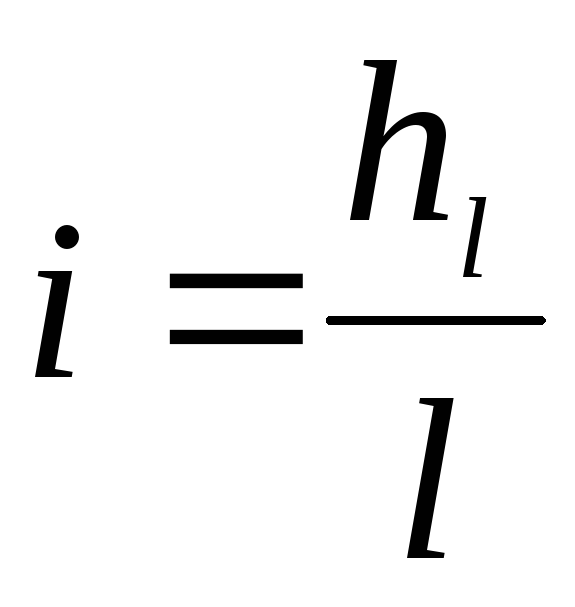 :
:
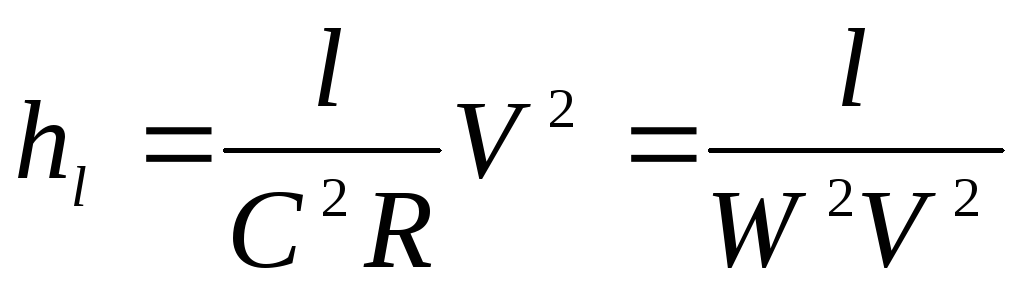 ; (4.42)
; (4.42)
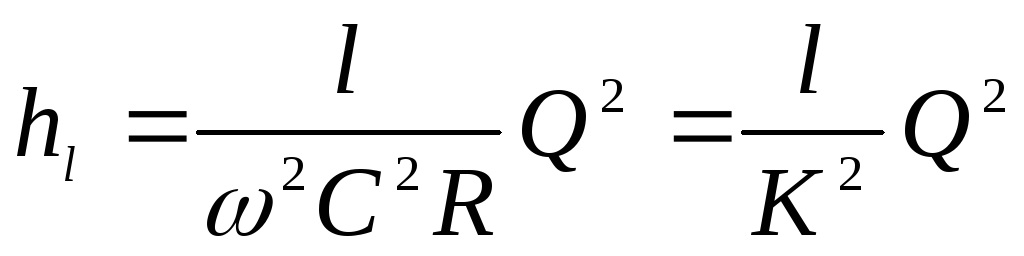 . (4.43)
. (4.43)
Удобно формулу потерь напора по длине для квадратичной области сопротивлений выразить через расход:
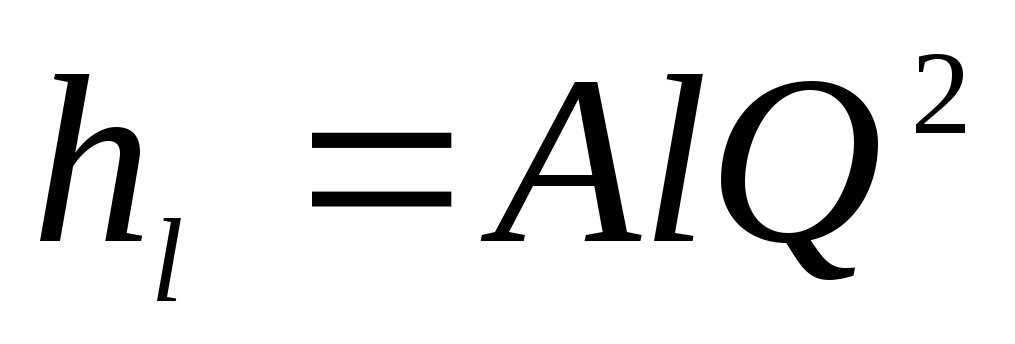 ; (4.44)
; (4.44)
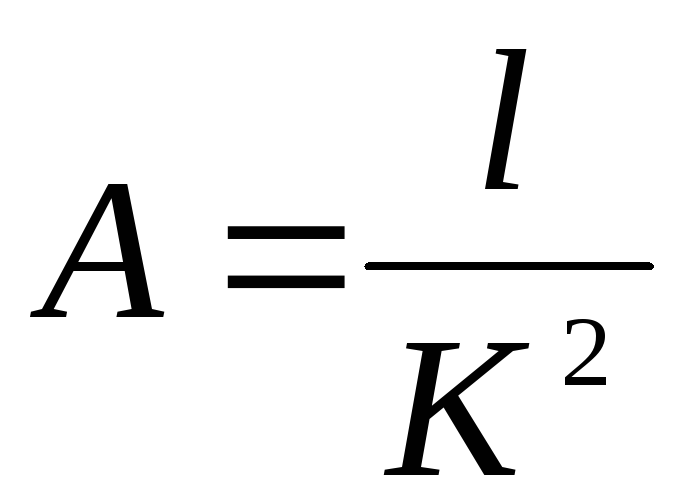 . (4.45)
. (4.45)
Параметр А получил название «удельное сопротивление».
Формула (4.44) называется трубопроводной формулой.
Трубопроводную
формулу можно получить, применив формулу
Вейсбаха-Дарси (4.33), выразив скорость
через расход, — 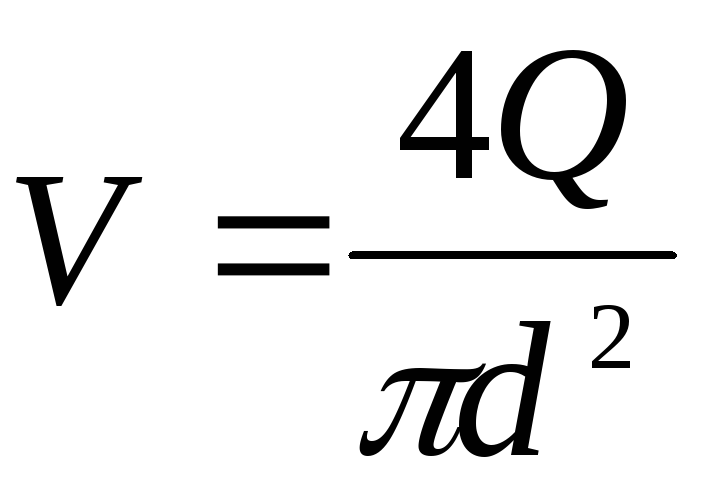 :
:
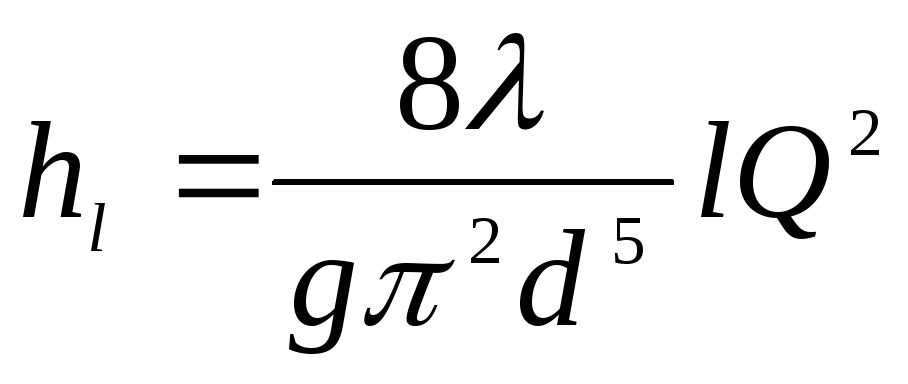 , (4-46)
, (4-46)
где
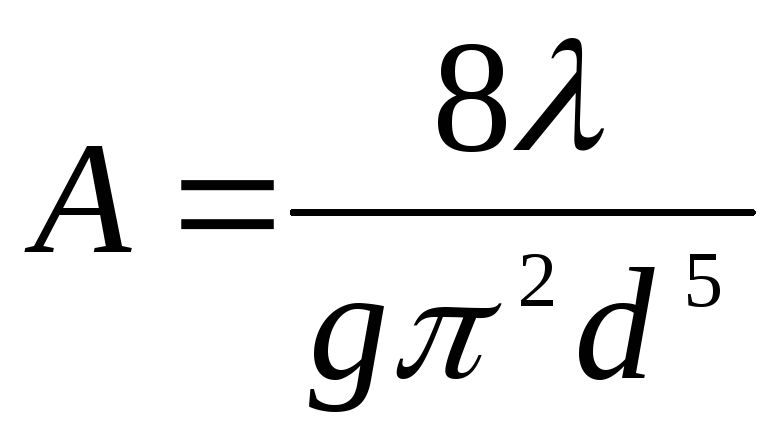 .
.
Используя зависимости
(4.44), (4.45) и (4.46), можно определить связь
коэффициента Шези С и коэффициента гидравлического трения  ,
приняв полное
наполнение жидкостью трубы
,
приняв полное
наполнение жидкостью трубы 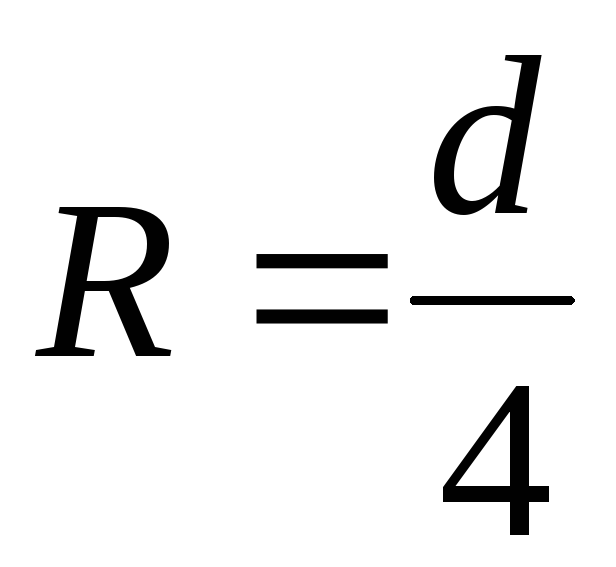 ,
,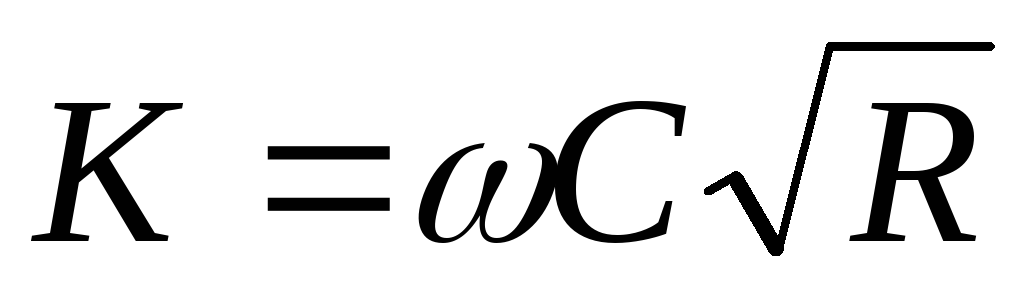 :
:
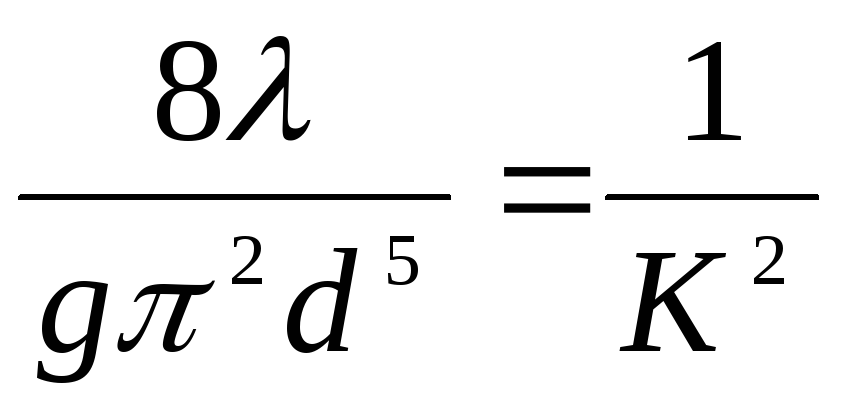 ;
; 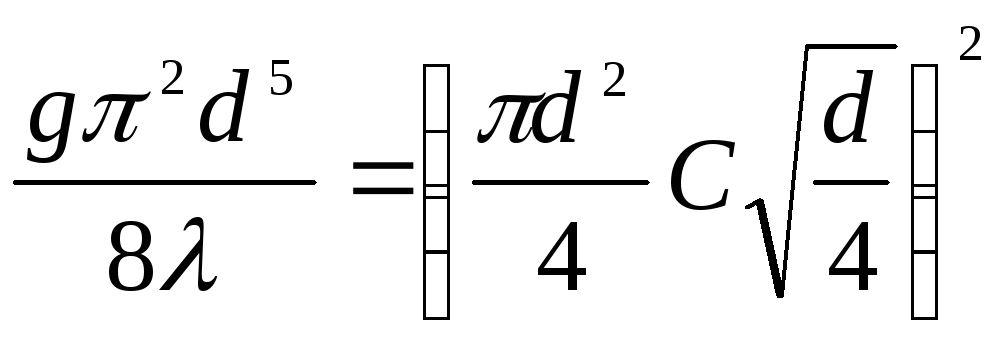 ,
,
откуда
 . (4.47)
. (4.47)
Понятие о гидравлических сопротивлениях, виды потерь напора (местные и по длине)
Потери удельной энергии (напора), или, как их часто называют, гидравлические потери, зависят от формы, размеров русла, скорости течения и вязкости жидкости, а иногда и от абсолютного давления в ней. Вязкость жидкости, хотя и является первопричиной всех гидравлических потерь, но далеко не всегда оказывает существенное влияние на их величину.
Гидравлические потери обычно разделяют на местные потери и потери на трение по длине.
Местные потери энергии обусловлены так называемыми местными гидравлическими сопротивлениями (рис 1.18), т.е. местными изменениями формы и размеры русла, вызывающими деформацию потока. При протекании жидкости через местные сопротивления изменяется её скорость и обычно возникают крупные вихри. Последние образуются за местом отрыва потока от стенок и представляют собой области, в которых частицы жидкости движутся в основном по замкнутым кривым или близким к ним траекториям.
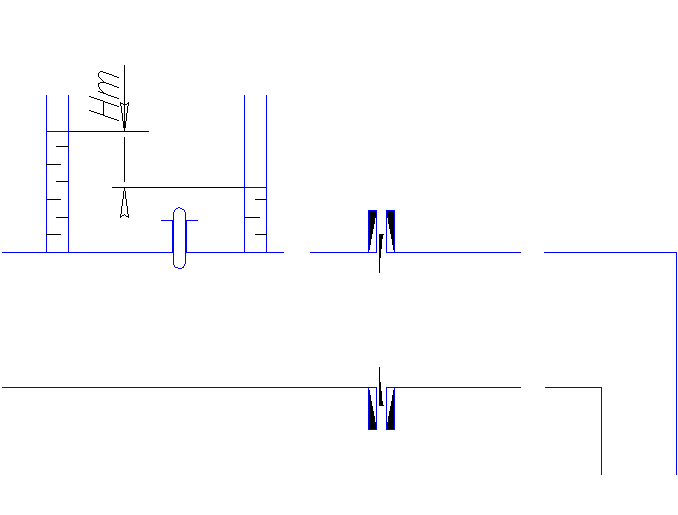
рис. 1.18 Пример местных гидравлических сопротивлений.
Местные сопротивления напора определяются по формуле следующим образом:
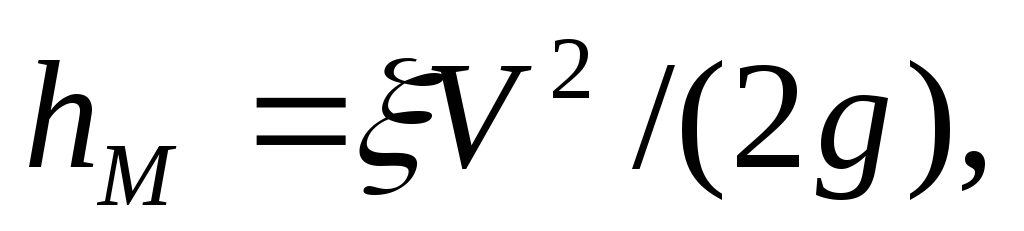 (1.51)
(1.51)
или в единицах давления
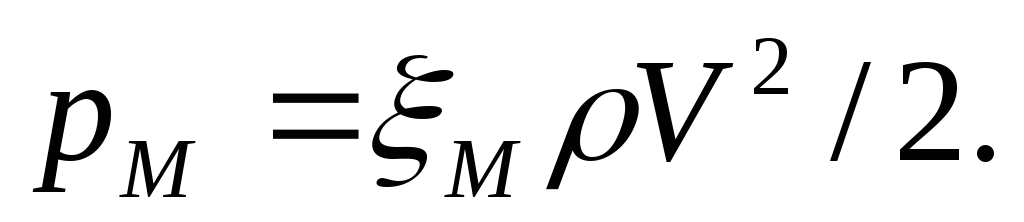 (1.52)
(1.52)
Выражение (1.5.4) часто называют формулой Вейсбаха. В ней V — средняя по сечению скорость в трубе, в которой установлено данное местное сопротивление.
Потери на трение по длине — это потери энергии, которые в чистом виде возникают в прямых трубах постоянного сечения, т.е. при равномерном течении, и возрастают пропорционально длине трубы. Рассматриваемые потери обусловлены внутренним трением в жидкости, а потому имеют место не только в шероховатых, но и в гладких трубах.
Потерю напора на трение можно выразить по общей формуле для гидравлического потерь, т.е.
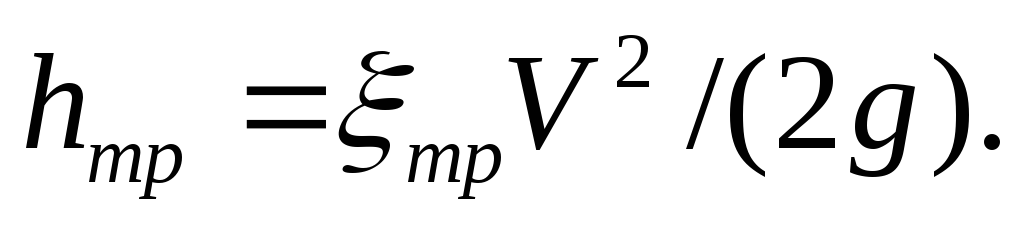 (1.53)
(1.53)
или
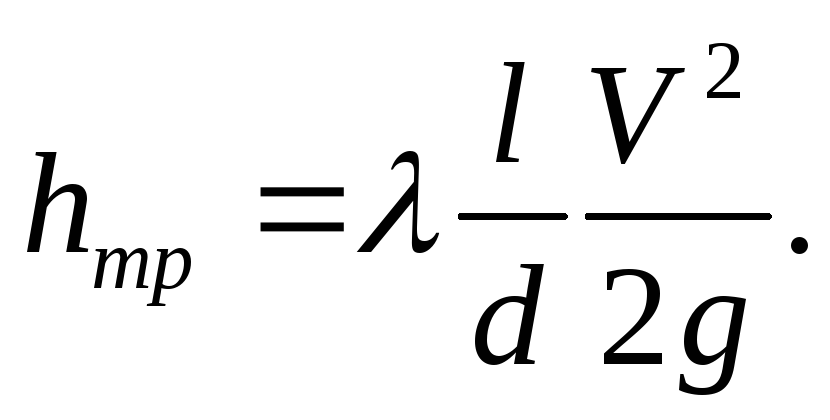 (1.54)
(1.54)
Общая формула для потерь напора по длине при установившемся равномерном движении жидкости. Коэффициент Дарси
Как показывают опыты, во многих, но не во всех случаях гидравлические потери приблизительно пропорциональны скорости течения жидкости во второй степени, поэтому в гидравлике принят следующий общий способ выражения гидравлических потерь полного напора в линейных единицах:
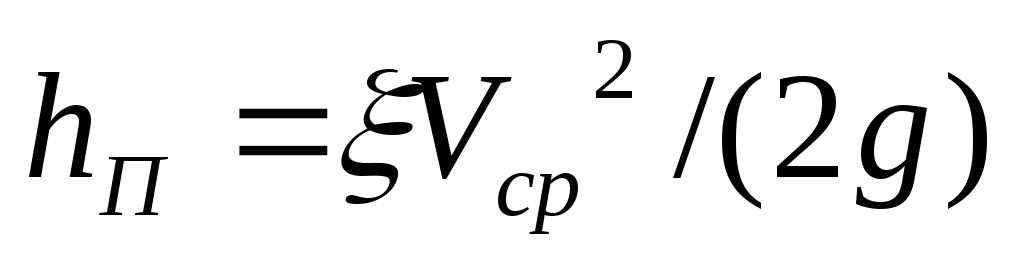 ,
или в единицах давления (1.55)
,
или в единицах давления (1.55)
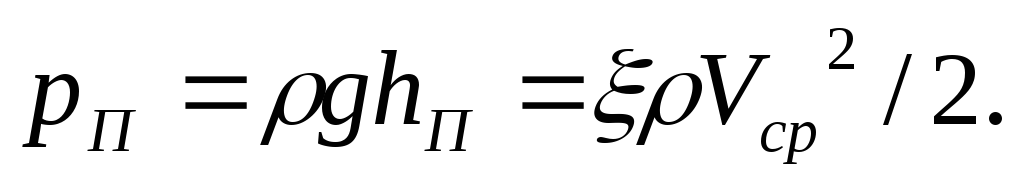 (1.56)
(1.56)
Такое выражение
удобно тем, что включает в себя безразмерный
коэффициент пропорциональности  ,
называемыйкоэффициентом
потерь Дарси или
коэффициентом сопротивления.
,
называемыйкоэффициентом
потерь Дарси или
коэффициентом сопротивления.
Основное уравнение равномерного движения
Выделим некоторый отсек элементарной струйки (рис. 1.19).
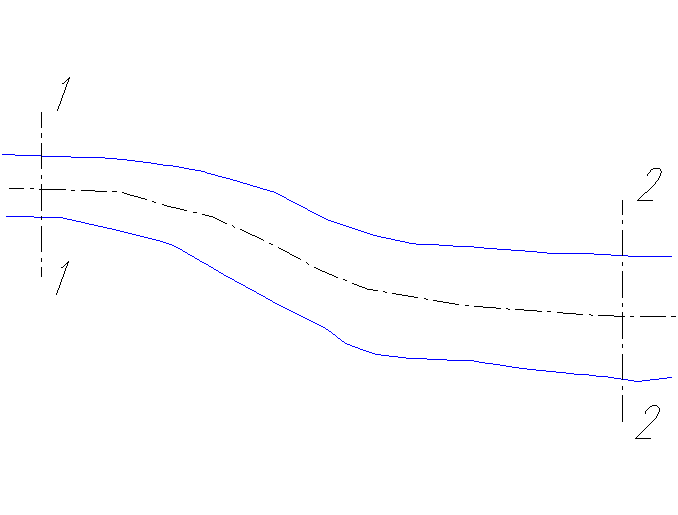
рис. 1.19 Объем элементарной струйки
Во вход в это сечение в единицу времени втекает определённый объём жидкости, равный
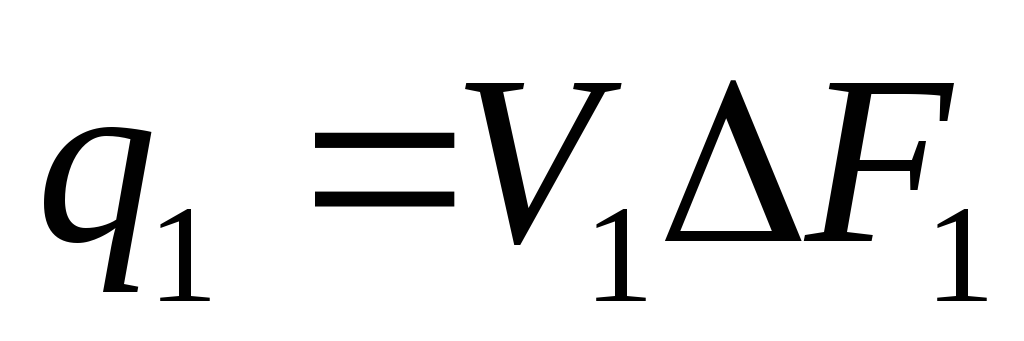 (1.57)
(1.57)
а через выход вытекает объём равный
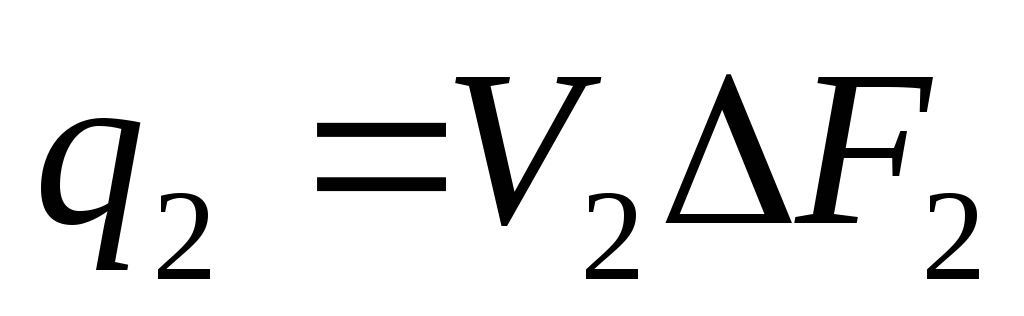 (1.58)
(1.58)
Примем, что жидкость несжимаема и что в ней невозможно образование незаполненных жидкостью пространств — пустот, т.е. будем считать, что соблюдается условие сплошности или неразрывности движения. Учитывая, что форма элементарной струйки с течением времени не изменяется и поперечный приток в струйку или отток из неё отсутствуют, приходим к выводу, что элементарные расходы жидкости, проходящие через вход и выход данного отрезка должны быть одинаковы. Таким образом,
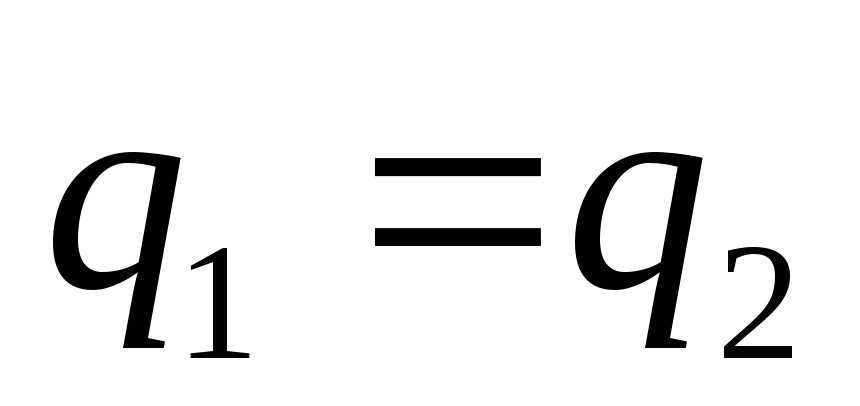 (1.59)
(1.59)
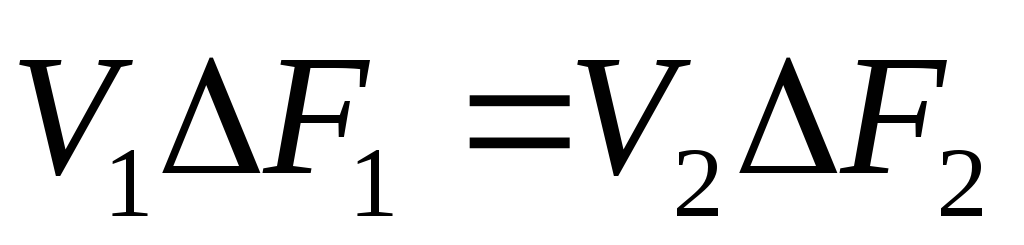 (1.60)
(1.60)
Подобные соотношения можно составить для любых отсеков элементарной струйки. Поэтому в более общем виде получаем, что всюду вдоль струйки
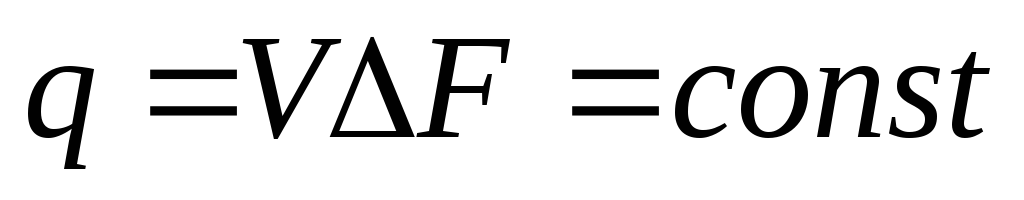 (1.61)
(1.61)
Полученное уравнение называется уравнением неразрывности; оно является первым основным уравнением гидродинамики.
Примеры решения задач
Задача 1. Найти потери напора по длине при движении воды с температурой t= 50°С в цельносварной стальной трубе, бывшей в употреблении, с внутренним диаметромd= 0,5 м. Расход водыQ=0,60 м3/с. Длина трубы 1=500 м.
Решение.
Находим по таблице [1] значение абсолютной эквивалентной шероховатости трубы kэ= 0,15 мм = 15 10-5м;kэ/d= 15 10-5/0,5 = 0,0003. Кинематический коэффициент вязкости для воды заданной температуры ν = 0,00556 см2/с.
С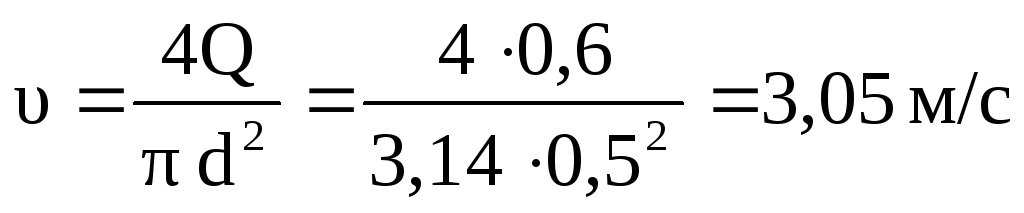 редняя
скорость течения воды в трубе
редняя
скорость течения воды в трубе
Ч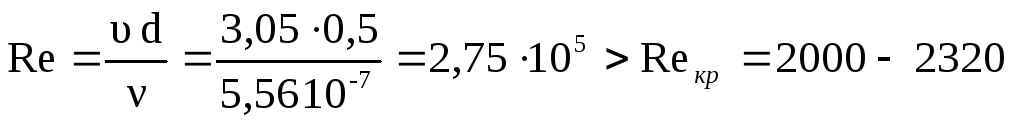 исло
Рейнольдса для потока воды в трубе
исло
Рейнольдса для потока воды в трубе
Режим движения турбулентный, поэтому коэффициента гидравлического трения находится по формуле (1)
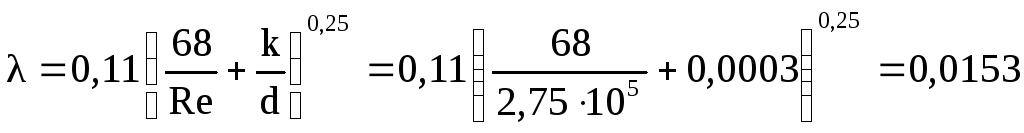
Потери напора по длине
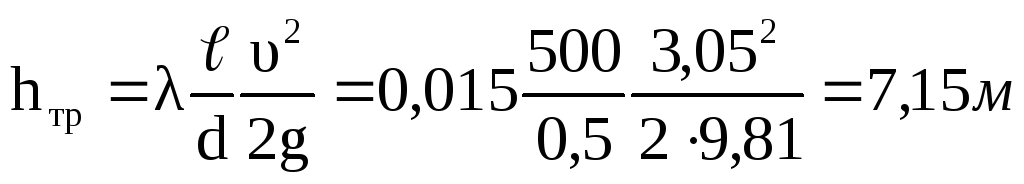 столба воды приt= 50°С.
столба воды приt= 50°С.
Плотность воды находим из табл. 1 ρ =988,07 кг/м3.
Потери полного давления по длине Δpтр= ρghтр= 988,07ּ9,81ּ7,15 = = 69,4ּ103Н/м2=69,4 кПа.
Задача 2. Найти потери напора по длине на один метр длинны при движении воздуха в бетонной трубе диаметром d=lм при давлении, близком к атмосферному, и температуреt= 20° С. Расход воздуха при заданных условияхQ= 15,6 м3/с
Решение
Заданному
состоянию воздуха соответствует
кинематический коэффициент вязкости
ν= 15,7 10-6м2/с
и п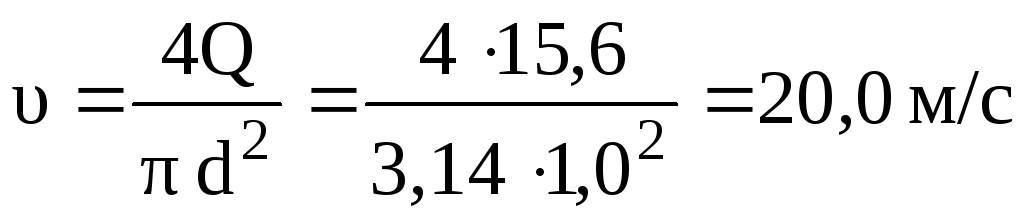 лотностьρ= 1,16 кг/м3
лотностьρ= 1,16 кг/м3
Н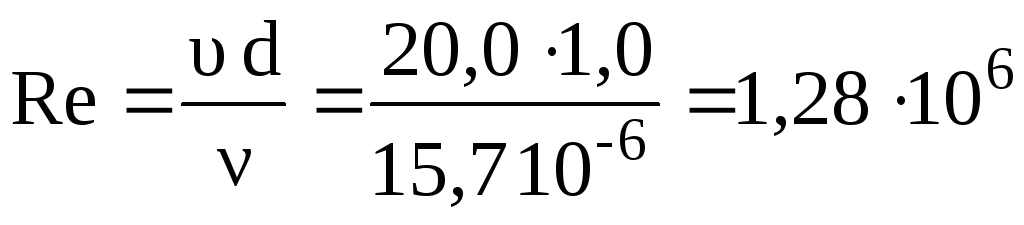 аходим
число Рейнольдса, характеризующее поток
воздуха в трубе
аходим
число Рейнольдса, характеризующее поток
воздуха в трубе
Определим относительную шероховатость трубопровода (при абсолютной эквивалентной шероховатости kэ= 0,5 мм):
Н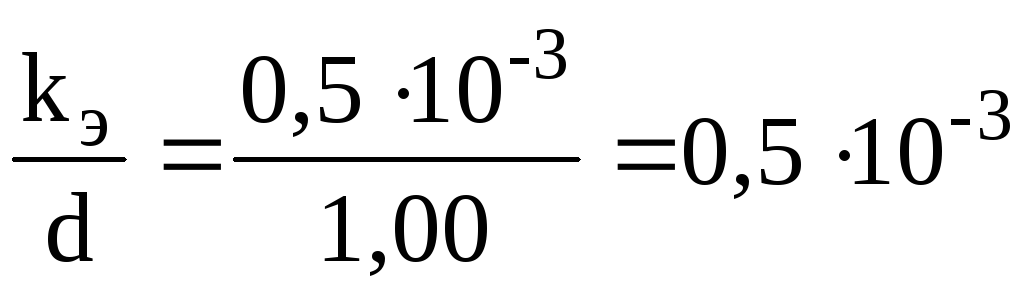 аходим
величину коэффициента гидравлического
трения по обобщенной формуле
аходим
величину коэффициента гидравлического
трения по обобщенной формуле

Определяем потерю полного давления на 1 пот. м трубы:
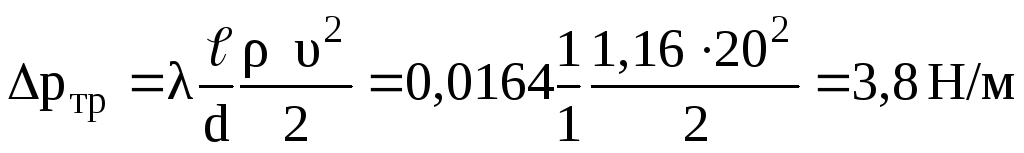
Задача 3. Определить величину потерь полного давления, вызванных резким поворотом трубопровода диаметром d= 200 мм на угол а = 90°. Трубопровод новый стальной, радиус поворотаR= 40 м. Жидкость — масло минеральное ν = 14,5 10-4м2/с. ρ = 880 кг/м3. Расход жидкостиQ= 0,5 м3/с.
Решение.
Потери полного давления в повороте находим по формуле Δр = ξ ρ υ2/2.
Коэффициент сопротивления поворота находим по формуле (5)
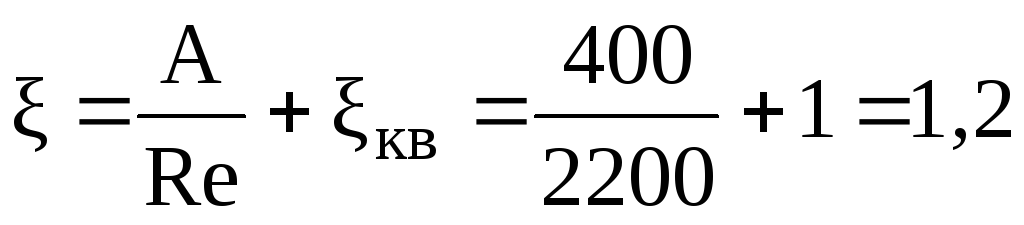
где ξкв— коэффициент сопротивления поворота ξкв= 1. Число Рейнольдса
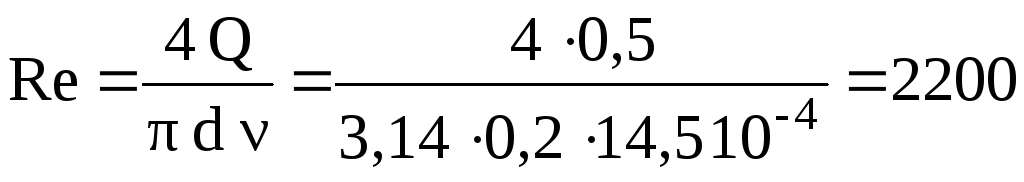
Из таблиц [1] коэффициент А =400,
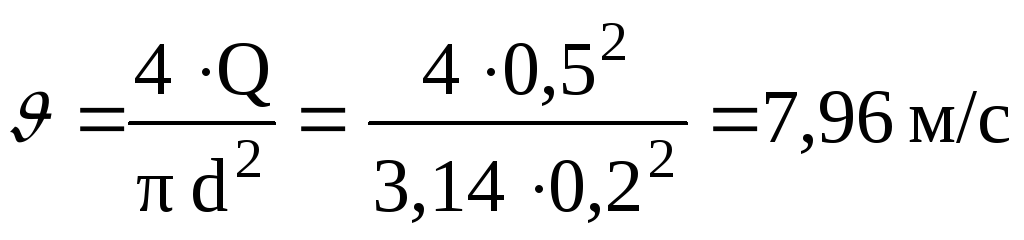
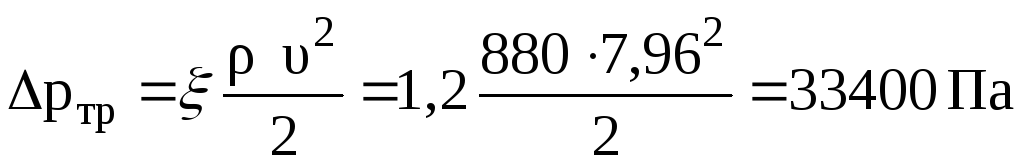
Задача 4. Определить расход минерального масла (плотностью ρ = 880 кг/м3,кинематической вязкостьюv= 10 10-4м2/с) при истечении в атмосферу через круглое отверстие диаметромd=2 см из резервуара, в котором давление (избыточное) р =5 105Н/м2.
Решение.
Определяем число Рейнольдса, характеризующее истечение,
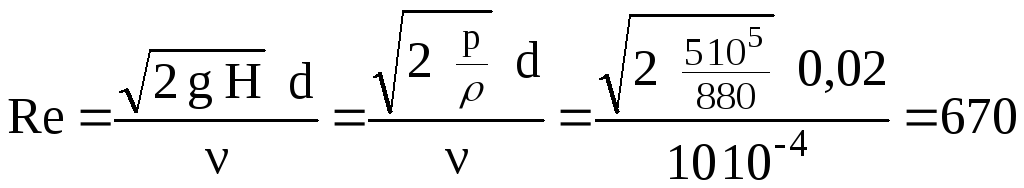
Из графика находим величину коэффициента расхода μ = 0,69. Определяем расход масла
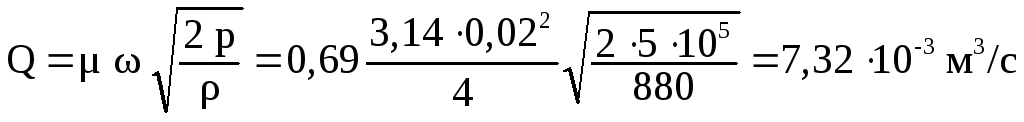
Задача 5. В дне сосуда имеется отверстие с закругленной кромкой d= 3 мм. Высота уровня воды в сосудеH=0,05 м. Определить скорость и расход при вытекании холодной (t1= 6°C) и горячей (t2= 99°С) воды из отверстия.
Решение.
Скорость вытекания воды из отверстия находим по формуле
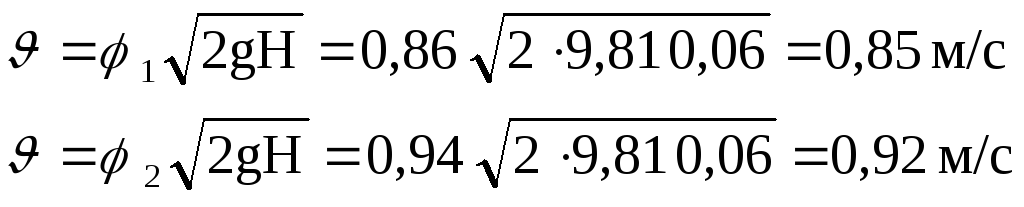
Коэффициент скорости φ находим из графика в функции от числа Рейнольдса, характеризующего истечение из отверстия.
Из таблиц [1] находим кинематический коэффициент вязкости воды.
ν1= 1, 47 10-6 м2/с;ν2= 0, 29 10-6 м2/с. Соответственно числа Рейнольдса будут равны
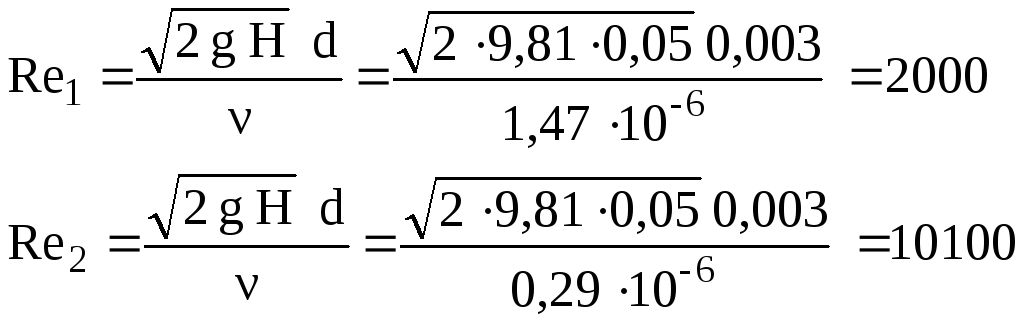
Из графика Альтшуля φ1= 0,86,φ2=0,94.
Скорость вытекания холодной воды v1= 0,98φ=0,98 0,86=0,85 м/с.
Скорость вытекания горячей воды v2=0,98 0,94=0,92 м/с.
Таким образом, горячая вода имеет скорость вытекания больше чем холодная, на (0,92 — 0,85)/0,85 100% = 8%, Это объясняется большей подвижностью (меньшей вязкостью) горячей воды.
Лекция 7 Классификация потерь напора
Одним из важнейших вопросов гидромеханики является определение потерь энергии при движении жидкости. При движении жидкости по трубопроводам возникают потери энергии, которые зависят от длины трубопроводов (пропорциональные длине канала) и потери энергии в местных сопротивлениях – запорная арматура, повороты, расширения и сужения трубопроводов – вызываемые изменениями скорости потока либо по величине, либо по направлению. Потери энергии потока как на преодоление сопротивлений по длине трубопроводов , так и на преодоление местных сопротивлений, в конечном счете обусловлены вязкостью жидкости, а, следовательно, теряемая механическая энергия рассеивается и переходит в тепловую.
Важность определения
потерь напора 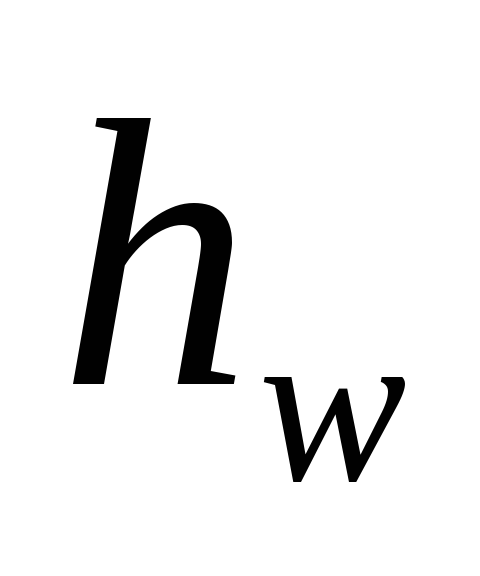 (или потерь давления
(или потерь давления )
связана с необходимостью расчета затрат
энергии, требуемых для компенсации этих
потерь при перемешивании жидкостей,
например, с помощью насосов, компрессоров
и т.д.
)
связана с необходимостью расчета затрат
энергии, требуемых для компенсации этих
потерь при перемешивании жидкостей,
например, с помощью насосов, компрессоров
и т.д.
Потерянный напор является суммой двух слагаемых:
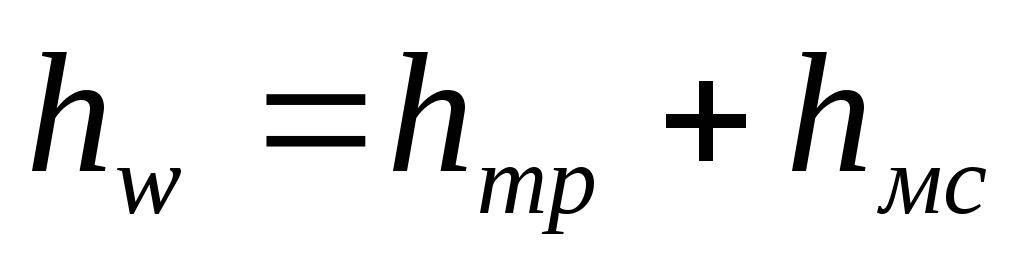 (98)
(98)
где 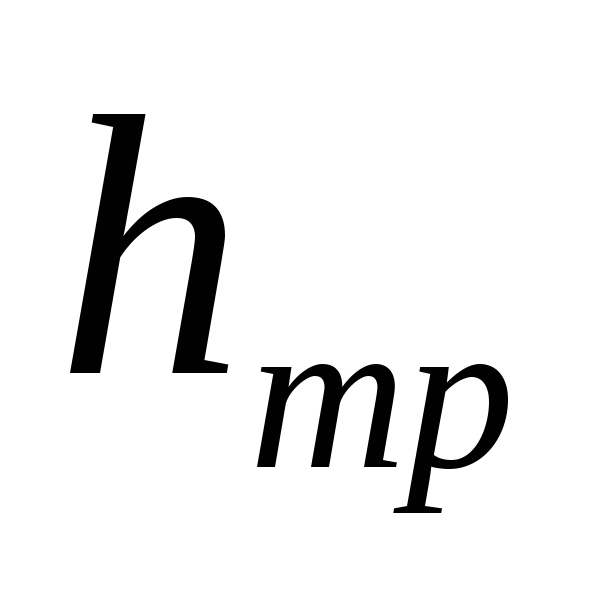 ,
,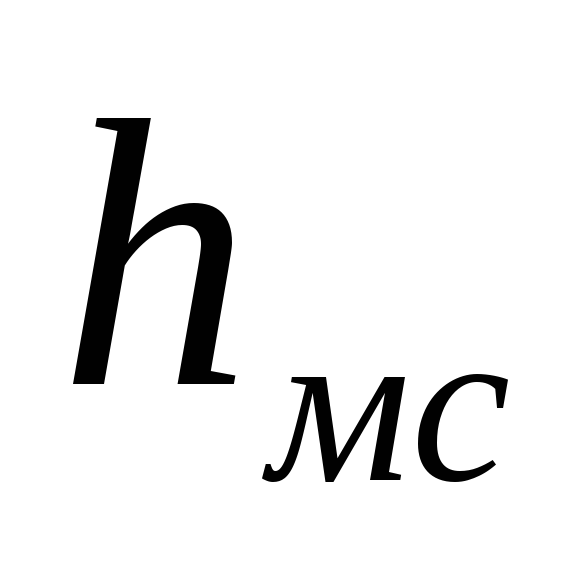 — потери напора вследствие трения и
местных сопротивлений, соответственно.
— потери напора вследствие трения и
местных сопротивлений, соответственно.
Для вычисления потерь напора при турбулентном режиме обычно пользуются частными эмпирическими формулами
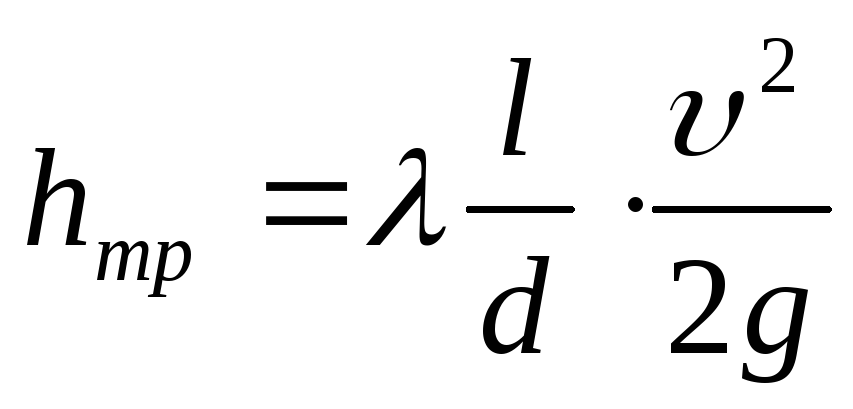 (99)
(99)
и
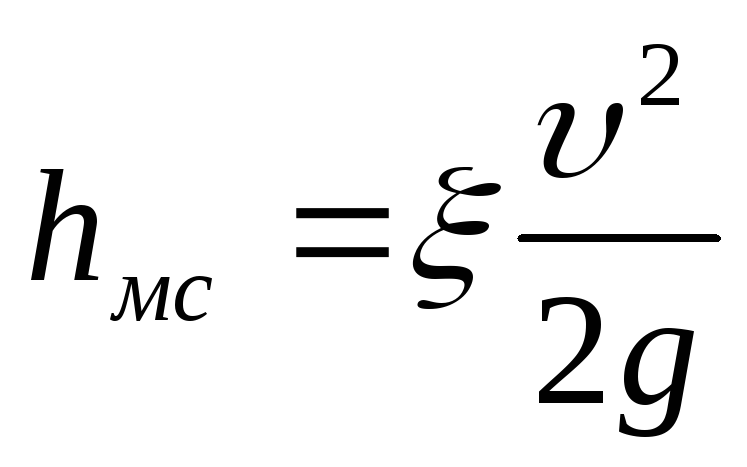 (100)
(100)
где |
| — коэффициент гидравлического трения; |
| — коэффициент местного сопротивления; | |
| —
длина трубопровода, | |
| —
диаметр трубы, | |
| —
средняя скорость движения жидкости
в трубопроводе, | |
| —
ускорение свободного падения, |
Средняя скорость, входящая в формулы (99) и (100) – эта такая, одинаковая для всех точек сечения скорость, при которой за единицу времени через данное сечение проходит тот же расход жидкости, что и при действительном распределении скоростей по сечению потока. Среднюю скорость определяют по уравнению расхода
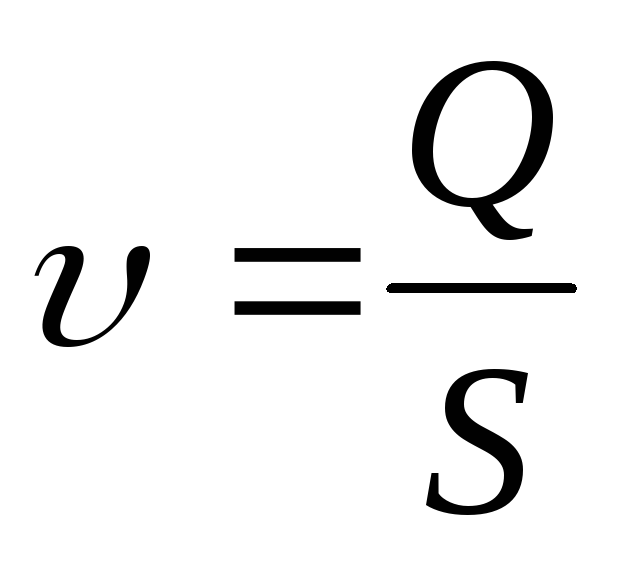 (101)
(101)
где |
| —
объемный расход, т.е. объем жидкости,
проходящий через живое сечение потока
за единицу времени, жидкости, |
| —
живое сечение потока (в случае течения
по трубе, равное площади поперечного
сечения трубы, |
Из формул (99) и
(100) следует, что потери энергии на трение
и местные сопротивления пропорциональны
скоростному и динамическому напору
(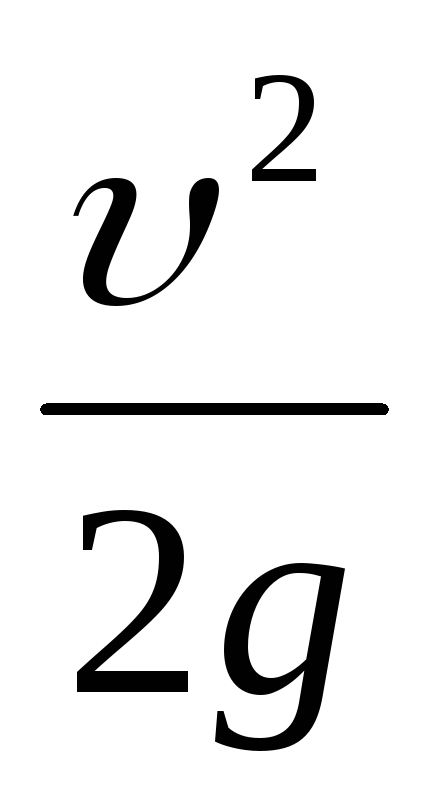 ),
который является мерой кинетической
энергии потока, отнесенной к единице
объема жидкости. В действительности
эта зависимость значительно сложнее,
так как коэффициент трения и коэффициент
местного сопротивления не являются
постоянными величинами, а существенно
зависят от скорости течения жидкости,
ее плотности и вязкости, а также диаметра
и шероховатости трубы, по которой
движется поток.
),
который является мерой кинетической
энергии потока, отнесенной к единице
объема жидкости. В действительности
эта зависимость значительно сложнее,
так как коэффициент трения и коэффициент
местного сопротивления не являются
постоянными величинами, а существенно
зависят от скорости течения жидкости,
ее плотности и вязкости, а также диаметра
и шероховатости трубы, по которой
движется поток.
Величина коэффициента
трения проявляется по-разному при
различных режимах движения потока в
трубе. В одном диапазоне чисел Рейнольдса,
характеризующих режим движения, на
величину  влияет в большей степени скорость, в
другом диапазоне преобладающее влияние
оказывают геометрические характеристики
– диаметр и шероховатость трубы (высота
выступов шероховатости
влияет в большей степени скорость, в
другом диапазоне преобладающее влияние
оказывают геометрические характеристики
– диаметр и шероховатость трубы (высота
выступов шероховатости ).
).
В связи с этим
различают четыре области сопротивления,
в которых изменение  имеет свою закономерность.
имеет свою закономерность.
Первая область – область ламинарного потока, ограниченная
значениями 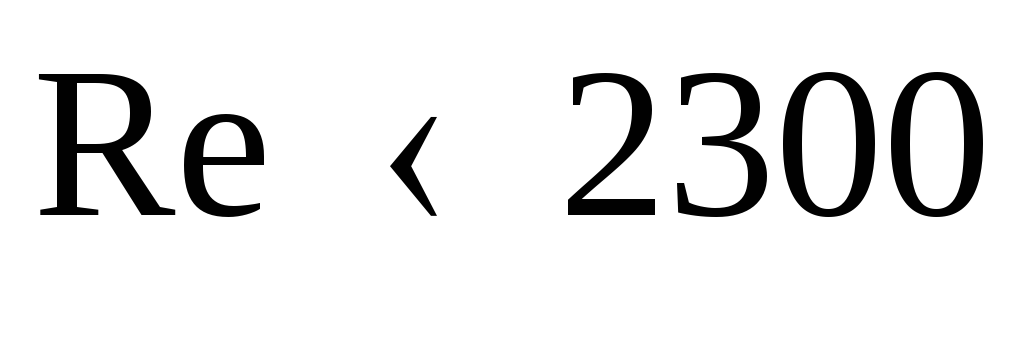 ,
в которой
,
в которой зависит от
зависит от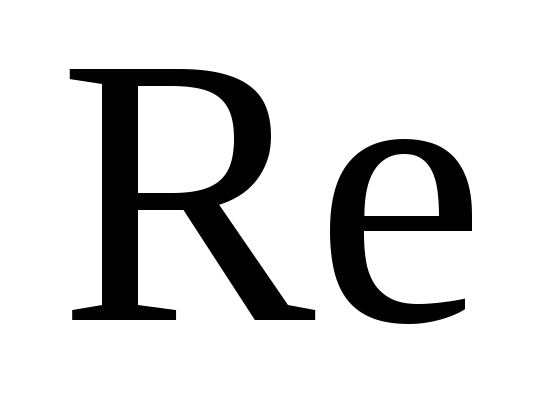 и не зависит от величины
и не зависит от величины ,
определяется по формуле Пуазеля
,
определяется по формуле Пуазеля
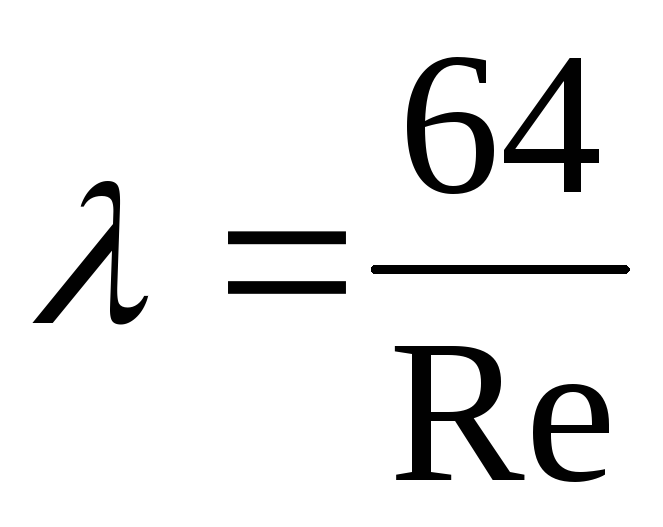 .
(102)
.
(102)
При этом значении  потери напора по длине трубы пропорциональны
скорости в первой степени. Все остальные
области сопротивления находятся в зоне
турбулентного режима с различной
степенью турбулентности.
потери напора по длине трубы пропорциональны
скорости в первой степени. Все остальные
области сопротивления находятся в зоне
турбулентного режима с различной
степенью турбулентности.
Вторая область – гидравлически гладкие трубы. Поток
в трубе при этом турбулентный, но у
стенок трубы сохраняется слой жидкости,
в пределах которого движение остается
ламинарным. Трубы считаются гидравлически
гладкими, если толщина ламинарного слоя  больше высоты выступов шероховатости
больше высоты выступов шероховатости .
В этом случае ламинарный слой покрывает
неровности стенок трубы и последние не
оказывают тормозящего влияния на
основное турбулентное ядро потока.
.
В этом случае ламинарный слой покрывает
неровности стенок трубы и последние не
оказывают тормозящего влияния на
основное турбулентное ядро потока.
Границу зоны гидравлически гладких труб можно определить из зависимости:
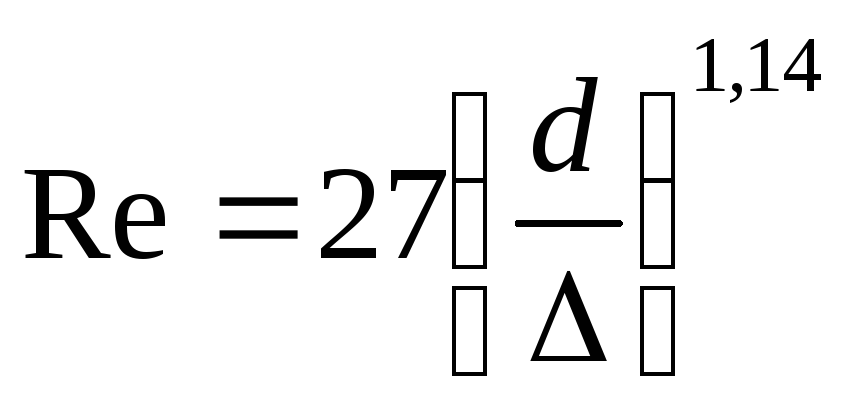 (103)
(103)
Для гидравлически
гладких труб, т.е при условии 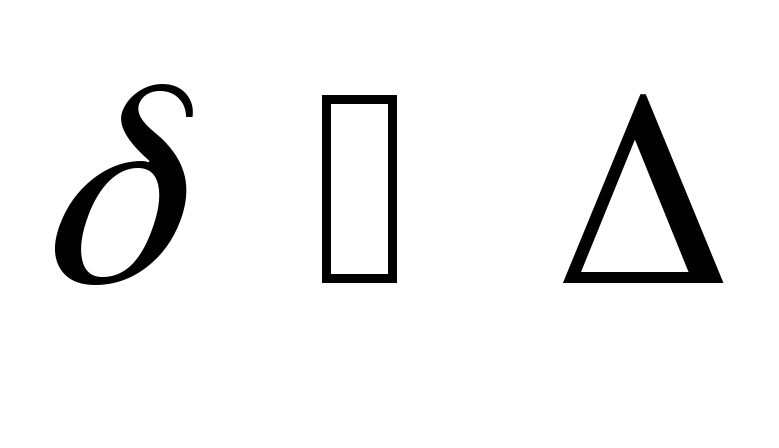 коэффициент
коэффициент может быть определен по формуле:
может быть определен по формуле:
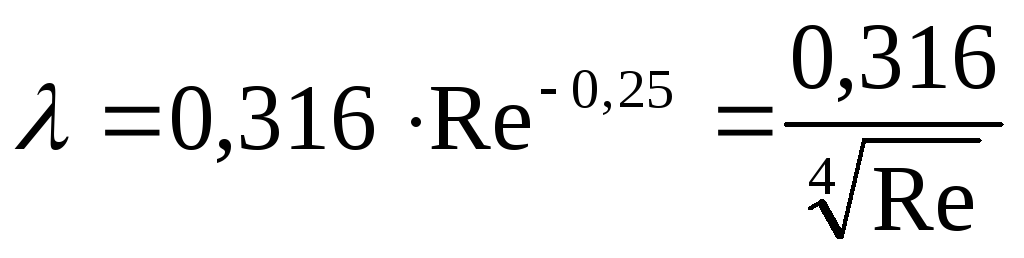 ,
(104)
,
(104)
которая применима
при значениях чисел Рейнольдса 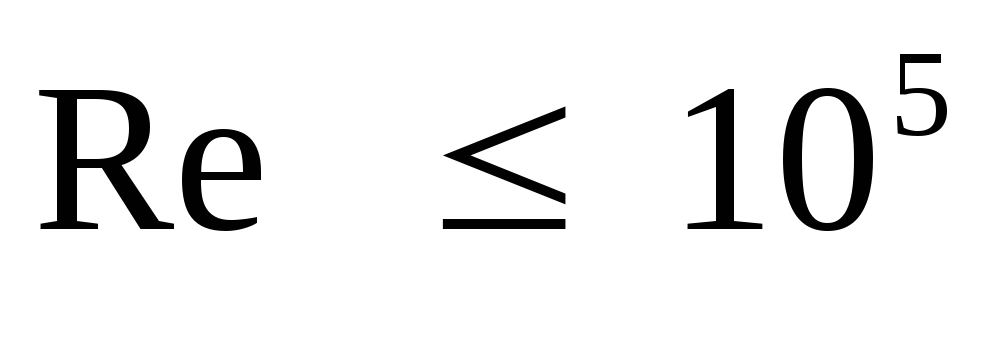 .
.
Третья область –
переходная от области гидравлически
гладких труб к квадратичной области. В
этой области толщина ламинарного слоя  равна или меньше выступов шероховатости
равна или меньше выступов шероховатости ,
которые в этом случае выступают как
препятствие у стенок, увеличивая
турбулентность, а, следовательно, и
сопротивление в потоке.
,
которые в этом случае выступают как
препятствие у стенок, увеличивая
турбулентность, а, следовательно, и
сопротивление в потоке.
Для определения  в переходной области сопротивления
применима формула
в переходной области сопротивления
применима формула
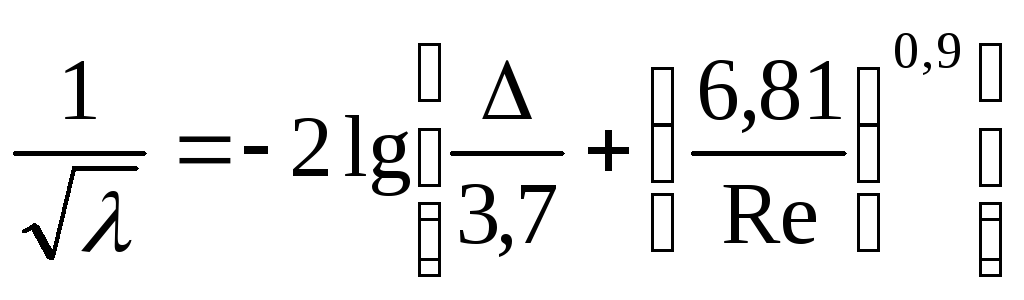 (105)
(105)
Потери напора по
длине трубы в переходной области
сопротивления пропорциональны скорости
в степени от 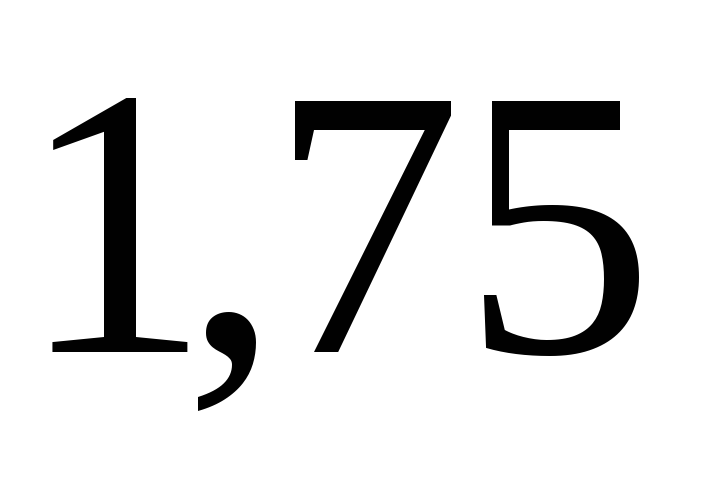 до
до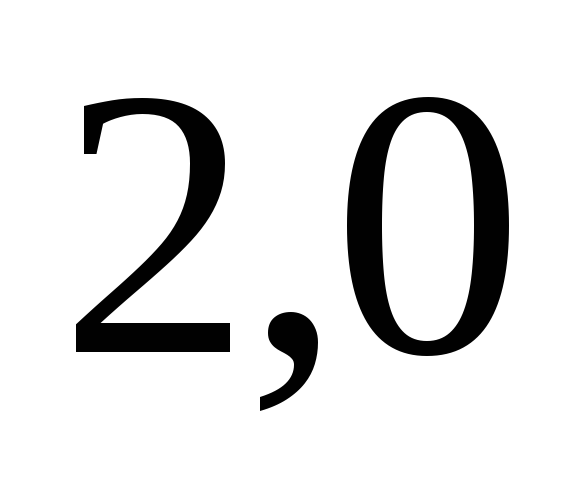 .
.
Четвертая область – гидравлически шероховатых труб или
квадратичного сопротивления (автомодельная
область). Основное влияние на сопротивление
потоку оказывает шероховатость стенок
трубы. Чем больше выступы шероховатости  ,
тем большую турбулентность они вызывают,
тем больше будут затраты энергии в
потоке на преодоление сопротивлений.
В квадратичной области сопротивления
коэффициент
,
тем большую турбулентность они вызывают,
тем больше будут затраты энергии в
потоке на преодоление сопротивлений.
В квадратичной области сопротивления
коэффициент не зависит от скорости, а становится
функцией только относительной
шероховатости
не зависит от скорости, а становится
функцией только относительной
шероховатости ,
выражаемой отношением абсолютной
шероховатости
,
выражаемой отношением абсолютной
шероховатости к диаметру трубы
к диаметру трубы
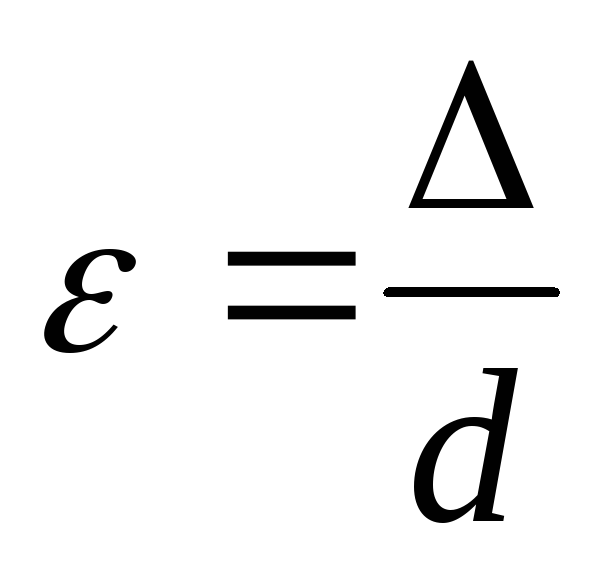 (106)
(106)
Для автомодельной области в уравнении (105) можно пренебречь вторым слагаемым в квадратных скобках, и оно принимает вид
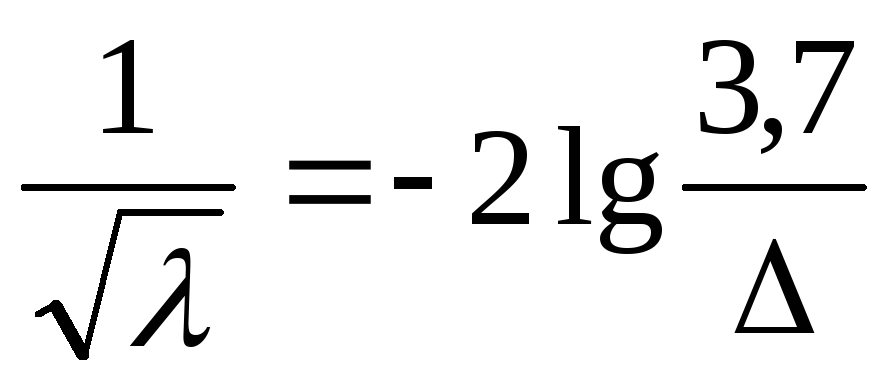 .
(107)
.
(107)
§ 5-3. Сложение потерь напора. Полный коэффициент сопротивления. Понятия длинных и коротких трубопроводов
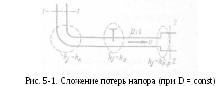
Представим
на рис. 5-1 для примера некоторый
трубопровод, имеющий по своей длине
различные «местные препятствия» (в виде
колена, задвижки, резкого расширения).
Считаем, что расстояние между этими
«препятствиями» достаточно велико:
более (20 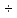 30)D
(при
этом взаимное
30)D
(при
этом взаимное
влияние имеющихся «препятствий» практически отсутствует; в противном случае оба «препятствия» следует рассматривать в совокупности — как одно).
Полная потеря напора hf на пути от сечения 1—1 до сечения 2 — 2 выразится в виде
hf=hl+Σhj.
Рассмотрим отдельно каждое слагаемое этого выражения.
1. Сумма местных потерь напора Σhj. Из рис. 5-1 видно, что
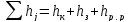 ,
(5-10)
,
(5-10)
где hк — местная потеря в колене; hз — местная потеря в задвижке; hр.р. — местная потеря при резком расширении.
Согласно Вейсбаху,
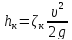 ;
; 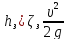 ;
;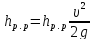 .
(5-11)
.
(5-11)
Следовательно,
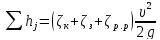 ,
(5-12)
,
(5-12)
или в общем случае
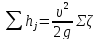 j (5-13)
j (5-13)
2. Потери напора по длине hl. Эти потери выражаются формулой (5-7). Введем обозначение:
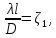 (5-14)
(5-14)
При этом hl представится в виде
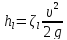 ,
(5-15)
,
(5-15)
где 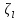 можно
назвать
коэффициентом
сопротивления
по
длине.
можно
назвать
коэффициентом
сопротивления
по
длине.
Как видно из (5-15), hl может быть выражена через скоростной напор.
3. Полная потеря напора hf. Подставляя в формулу (5-9) зависимости (5-13) и (5-15), получаем:
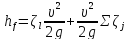 (5-16)
(5-16)
или
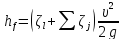 .
(5-17)
.
(5-17)
Вводя обозначение
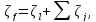 (5-18)
(5-18)
получаем, что
(5-19)
Это и есть окончательная формула для расчета п о л н ы х потерь напора (когда учитывают величину hl и величину Σhj).
Как видно, hf также выражается через скоростной напор.
Новый коэффициент ζf, учитывающий все потери напора на данной длине потока, назовем полным коэффициентом сопротивления.
Таким образом, на протяжении всего изложения, касающегося определения потерь напора в трубах, было введено три разных коэффициента сопротивления:
а) коэффициент местного сопротивления ζj для учета hj;
б) коэффициент сопротивления по длине ζl для учета hl;
в) полный коэффициент сопротивления ζf для учета hf.
При помощи этих коэффициентов соответствующие потери напора вы- ражаются через скоростной напор.
Случай трубопровода переменного диаметра. Выше величину hf мы выражали через среднюю скорость υ, имея трубу постоянного диаметра, что позволило величину скоростного напора в зависимостях (5-12) и (5-17) выносить за скобки.
Положим,.что нам задан трубопровод переменного диаметра (рис. 5-2). Возникает вопрос, как в этом случае будут преобразовываться формулы (5-12) и (5-17).
Рассмотрим для примера сумму двух местных потерь, из которых первая (на резкое расширение) выражается через υ1 и вторая (на задвижку) — через υ2:
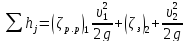 .
(5-20)
.
(5-20)
Первую местную потерю легко можно выразить также и через υ2. Действительно,
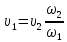 ;
(5-21)
;
(5-21)
следовательно
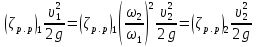 (5-22)
(5-22)
где
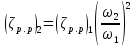 .
(5-23)
.
(5-23)
Таким
образом,
видно,
что
все
слагаемые,
входящие
в
выражение Σhj,
могут
быть
всегда
выражены
через
одну
и
ту
же
скорость,
даже
если
труба
будет
переменного
диаметра.
При
этом
придется
изменять
только
величины 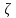 :
умножить
их
на
квадрат
отношения
с оответствующих
площадей
ω.
:
умножить
их
на
квадрат
отношения
с оответствующих
площадей
ω.
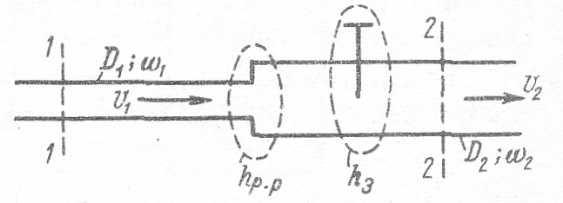
Рис. 5-2. Сложение потерь напора (при D ≠ const)
Выразив все слагаемые в формуле (5-12) или (5-17) через одну и ту же скорость υ, можем выносить в этих формулах скоростной напор за скобки так же, как и в случае трубопровода постоянного диаметра.
Понятия «длинного» и «короткого» трубопроводов. В случае достаточно длинных водопроводных труб величина Σhjпо сравнению с величиной hl оказывается пренебрежимо малой, причем получается, что
hf ≈hl.
Такие трубы принято называть «длинными» в отличие от так называемых «коротких» труб, когда при расчете, помимо потерь напора по длине hhприходится учитывать еще местные потери напора Σhj.
В случае «длинных» трубопроводов при построении линий Е—Е и Р—Р обычно пренебрегают также и скоростным напором (ввиду его малости), считая, что напорная и пьезометрическая линии совпадают. Линия, в которую сливаются линии Е—Е и Р —Р, в этом случае обычно называется пьезометрической линией.
Принято считать, что в случае городских водопроводных труб (диаметром до 200—500 мм) длинный трубопровод получается, когда его длина более 200—1000 м. При меньшей длине местные потери напора часто могут составлять уже величину более 3 — 5% от потерь hl, причем их приходится учитывать.



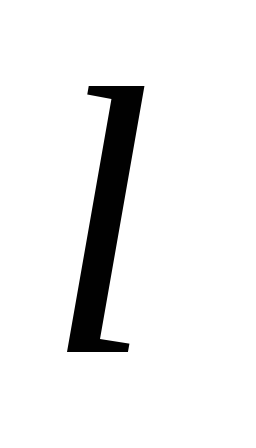
 ;
;
 ;
;
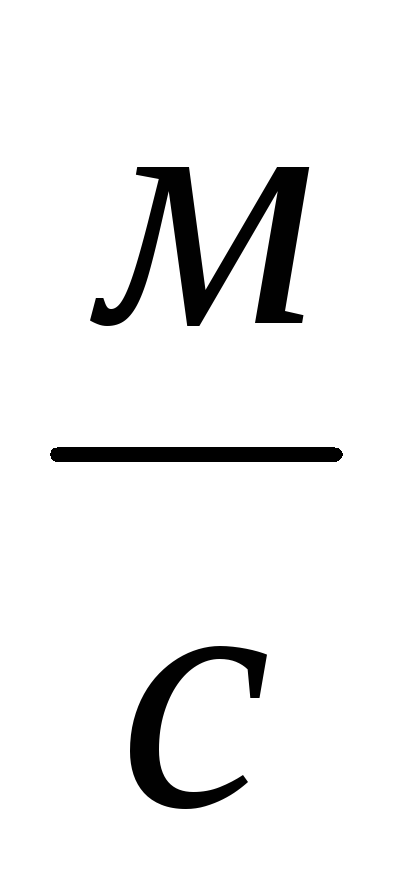 ;
;
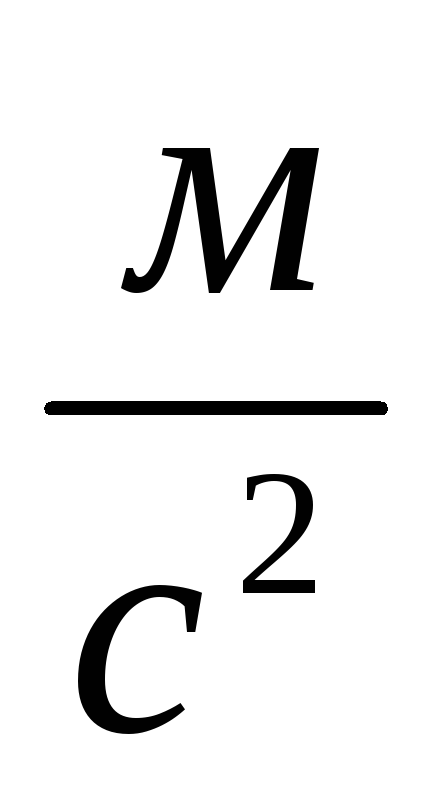 .
.
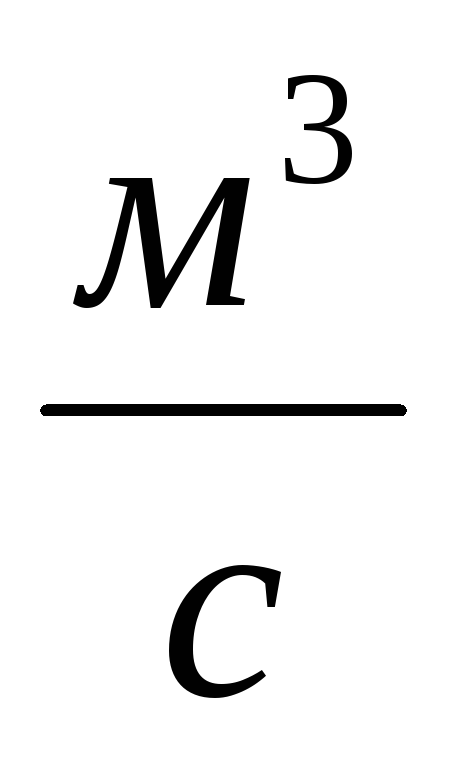 ;
;
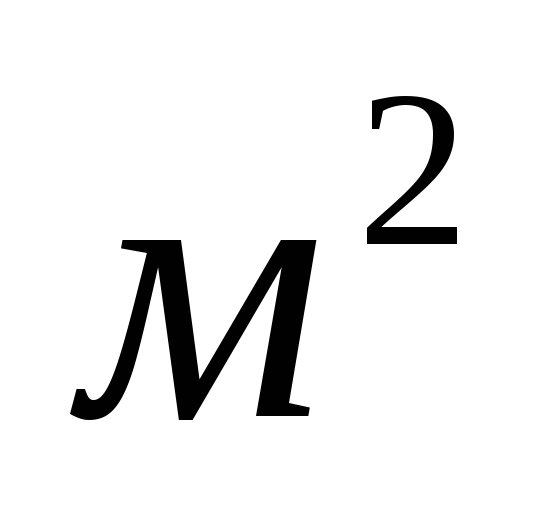 .
.