Гидравлические потери — Википедия
Гидравлические потери или гидравлическое сопротивление — безвозвратные потери удельной энергии (переход её в теплоту) на участках гидравлических систем (систем гидропривода, трубопроводах, другом гидрооборудовании), обусловленные наличием вязкого трения[1][2]. Хотя потеря полной энергии — существенно положительная величина, разность полных энергий на концах участка течения может быть и отрицательной (например, при эжекционном эффекте).
Гидравлические потери принято разделять на два вида:
- местные гидравлические потери — обусловлены т. н. местными гидравлическими сопротивлениями — изменениями формы и размера канала, деформирующими поток. Примером местных потерь могут служить: внезапное расширение трубы, внезапное сужение трубы, поворот, клапан и т. п.
Гидравлические потери выражают либо в потерях напора Δh{\displaystyle \Delta h} в линейных единицах столба среды, либо в единицах давления ΔP{\displaystyle \Delta P}: Δh=ΔPρg{\displaystyle \Delta h={\Delta P \over \rho g}}, где ρ{\displaystyle \rho } — плотность среды,
Во многих случаях приближённо можно считать, что потери энергии при протекании жидкости[3] через элемент гидравлической системы пропорциональны квадрату скорости жидкости[2]. По этой причине удобно бывает характеризовать сопротивление безразмерной величиной ζ[4], которая называется коэффициент потерь или коэффициент местного сопротивления и такова, что
- Δp=ζρw22, Δh=ζw22g.{\displaystyle \Delta p=\zeta {\rho w^{2} \over 2}{\mbox{, }}\Delta h=\zeta {w^{2} \over 2g}{\mbox{.}}}
То есть в предположении, что скорость w по всему сечению потока одинакова, ζ=Δp/eторм, где eторм = ρw²/2 — энергия торможения единицы объёма потока относительно канала. Реально в потоке скорость жидкости не равномерна, в справочной литературе в данных формулах принимается среднерасходная скорость w=Q/F, где Q — объёмный расход, F — площадь сечения, для которого рассчитывается скорость[1]. Таким образом, средняя энергия торможения потока обычно несколько больше ρw²/2, см. Среднее квадратическое.
Для линейных потерь обычно пользуются коэффициентом потерь на трение по длине (также коэффициент Дарси) λ, фигурирующего в формуле Дарси — Вейсбаха[2]
- Δh=λLd⋅w22g{\displaystyle \Delta h=\lambda {\frac {L}{d}}\cdot {w^{2} \over 2g}},
где L — длина элемента, d — характерный размер сечения (для круглых труб это диаметр). Иначе в единицах давления
- Δp=λLd⋅ρw22{\displaystyle \Delta p=\lambda {\frac {L}{d}}\cdot {\rho w^{2} \over 2}};
таким образом, для линейного элемента относительной длины L/d коэффициент сопротивления трения ζтр=λL/d.
Влияние режима течения в трубах на гидравлические потери[править | править код]
Поскольку при турбулентном режиме течения происходит расход энергии потока на преодоление вязкости при турбулентных колебаниях, гидравлические потери при ламинарном режиме течения жидкости значительно меньше, чем при турбулентном. Так, например, если бы в системах водоснабжения и отопления при существующих скоростях движения жидкостей возможно было бы поддерживать ламинарный режим течения, то напор насосов можно было бы уменьшить в 5—10 раз[источник не указан 2800 дней]. Изменение режима течения с ламинарного на турбулентный вызывает скачкообразное увеличение сопротивления (при некоторых скоростях, т.е. в некотором диапазоне чисел Рейнольдса, ламинарное течение неустойчиво, но в определённых условиях может существовать). В то же время коэффициент гидравлического сопротивления при ламинарном режиме обычно получается больше, чем при турбулентном, поскольку для ламинарных режимов характерны более низкие скорости. При ламинарном режиме сопротивление примерно линейно зависит от скорости (соответственно, коэффициент примерно линейно падает, например, в круглых трубах λ=64Re{\displaystyle \lambda ={\frac {64}{\mathrm {Re} }}}). При турбулентном режиме в гидравлически гладких трубах (при небольших шероховатостях и небольших Re) зависимость имеет иной характер (для круглых труб λ=0,3164Re4.{\displaystyle \lambda ={\frac {0,3164}{\sqrt[{4}]{\mathrm {Re} }}}.}) и во всех практически реализуемых случаях лежит выше зависимости для ламинарного режима; при бо́льших числах Рейнольдса под влиянием шероховатости график λ претерпевает сложный изгиб, и начиная с некоторого критического значения при Re>Reкр (область автомодельности) λ зависит только от шероховатости.
На преодоление гидравлических потерь в различных технических системах затрачивается работа таких устройств, как насосы, воздуходувки.
Для уменьшения гидравлических потерь рекомендуется в конструкциях гидрооборудования избегать применения деталей, способствующих резкому изменению направления потока — например, заменять внезапное расширение трубы постепенным расширением (диффузор), придавать телам, движущимся в жидкостях, обтекаемую форму и др. Даже в абсолютно гладких трубах имеются гидравлические потери[2]; при ламинарном режиме шероховатость мало на них влияет, однако при обычных в технике турбулентных режимах её увеличение, как правило, вызывает рост гидродинамического сопротивления.
Иногда, напротив, требуется ввести гидравлическое сопротивление в поток. Для этого применяются дроссельные шайбы, редукционные установки, регулирующие клапаны. По измерению давления на некотором элементе, график коэффициента гидравлического сопротивления которого известен, можно узнать скорость потока в некоторых распространённых типах расходомеров.
- ↑ 1 2 Идельчик И. Е. Справочник по гидравлическим сопротивлениям/ Под ред. М. О. Штейнберга. — 3-е изд., перераб. и доп.— М.: Машиностроение, 1992. — C. 10
- ↑ 1 2 3 4 Гидравлика, гидромашины и гидроприводы: Учебник для машиностроительных вузов / Т. М. Башта, С. С. Руднев, Б. Б. Некрасов и др.. — 2-е изд., перераб.. —
- ↑ В гидродинамике жидкостью называется любая текучая среда, как капельная жидкость, так и газ.
- ↑ Также применяется обозначение ξ; буквы часто путают, иногда применяют для различения того, во входном или выходном сечении элемента измерялась скорость в формуле (для расширяющихся или сужающихся элементов).
11. Потери напора по длине. Порядок определения коэффициента трения.
Потери напора по длине иначе называют потерями напора на трение, возникают в гладких прямых трубах с постоянным сечением при равномерном течении. Такие потери обусловленны внутренним трением в жидкости и поэтому происходит и в шероховатых трубах, и в гладких. Основной расчетной формулой для потерь напора при ламинарном и турбулентном режиме движения в круглых трубах является
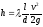
V-средняя скорость движения
Коэффициент
трения зависит от числа Рейнольдса и
от безразмерного геометрического
фактора- относительной шероховатости 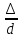 (
(
Коэффициент
трения при ламинарном режиме движения
жидкости 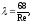
Область турбулентного и переходного режимов разбиваются на 3 области :
1)
область гидравлически гладких труб 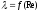
2)
область доквадратического сопротивления
шероховатых труб 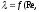

3)
область квадратичного сопротивления
шероховатых труб 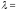
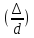
При
турбулентном режиме движения жидкости
коэффициент движения определяется по
графику Мурина и по формуле Альтшуля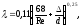
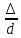 относительная
шероховатость трубопровода
относительная
шероховатость трубопровода
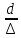 относительная
гладкость трубопровода
относительная
гладкость трубопровода
Величину абсолютной эквивалентной шероховатости при расчетах берут из справочника в зависимости от материала труб и состояния его внутренней поверхности.
12.Местные гидравлические сопротивления. Потери напора на местных сопротивлениях.
Местные сопротивления это такие участки трубопровода, на которых происходит деформация потока, т.е. происходит изменения скорости потока или по величине или по направлению.
К местным сопротивлениям относятся: вход и выход потока из трубы, внезапные сужения и расширения труб, плавные сужения и расширения труб колена, отводы, тройники, диафрагмы, регулирующие устройства (краны, вентили, задвижки и т.д)
Протекая через местное сопротивление, поток деформируется, возникают пульсации скоростей и давлений, образуются вихревые зоны с обратными токами вследствие отрыва потока от стенок трубопровода. На эти процессы смешения и вихреобразования тратится часть полной энергии потока, которая превращается в тепло и рассеивается в окружающее пространство.
Различают четыре вида местных сопротивлений
Местные сопротивления на которых происходит изменение скорости по величине (рис.25 на стр.52)
Местные сопротивления связанные с изменением направления движения жидкости (рис. 26 на стр.52)
Местные сопротивления на которых происходит смешение или разделение потока(рис.27 на стр. 53)
Трубопроводная арматура(краны, вентили, задвижки, расходомеры и т.п.)
Потери напора на местном сопротивлении рассчитываются в долях от величины скоростного напора:
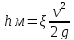
где -коэффициент
местного сопротивления,
-коэффициент
местного сопротивления,
v-скорость движения жидкости, м/с
g-ускорение свободного падения, м/с^2
13.Виды потерь напора(давлений) в трубопроводах. Расчетные формулы.
Потери напора по длине потока. Иначе их называют потерями напора на трение, возникают в гладких прямых трубах с постоянным сечение при равномерном течении. Такие потери обусловлены внутренним трением в жидкости и поэтому происходят в шероховатых трубах, и в гладких.
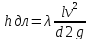
где -коэффициент гидравлического трения,
l-длина трубопровода, м;
d-диаметр трубопровода, м;
v-средняя скорость движения жидкости, м/с;
g-ускорение свободного падения, м/с^2;
коэффициент
трения 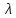 зависит от числа РейнольдсаRe(режима
движения жидкости) и от безразмерного
геометрического фактора-относительной
шероховатости
зависит от числа РейнольдсаRe(режима
движения жидкости) и от безразмерного
геометрического фактора-относительной
шероховатости  (или
(или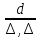 -абсолютное
значение эквивалентной шероховатости)
-абсолютное
значение эквивалентной шероховатости)
коэффициент трения при ламинарном режиме движения жидкости рассчитывается по формуле:
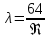
На практике при турбулентном режиме движения коэффициент трения может быть определен по графику Г.А.Мурина или рассчитан по формуле А.Д.Альтшуля:
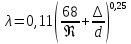
Где Re-критерий Рейнольдса;
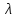 -коэффициент
трения;
-коэффициент
трения;
 -абсолютное
значение эквивалентной шероховатости,
м;
-абсолютное
значение эквивалентной шероховатости,
м;
d- диаметр трубопровода, м;
Потери напорана местное сопротивления.
Потери напора на местном сопротивлении рассчитываются в долях от величины скоростного напора:
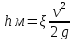
где -коэффициент
местного сопротивления,
-коэффициент
местного сопротивления,
v-скорость движения жидкости, м/с
g-ускорение свободного падения, м/с^2
Принцип сложения потерь напора.
Как правило, трубопроводы имеют прямые участки и множество местных сопротивлений. Принцип сложения потерь напора заключается в том, что потери напора по длине и потери напора на местных сопротивлениях складываются, т.е общие потери напора:
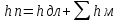
т.е 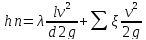
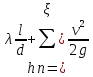
где где 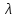 -коэффициент
гидравлического трения,
-коэффициент
гидравлического трения,
l-длина трубопровода, м;
d-диаметр трубопровода, м;
v-средняя скорость движения жидкости, м/с;
g-ускорение свободного падения, м/с^2;
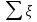 -сумма
коэффициентов местных сопротивлений.
-сумма
коэффициентов местных сопротивлений.
Часто
в расчетах требуется определить потерю
давления 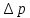 .
.
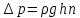
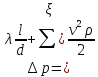
Потеря давления в трубопроводе на трение(для участка прямого трубопровода, длинного трубопровода), вычисляется по формуле
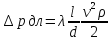
8.Потери напора в трубопроводе
При перекачке нефти по магистральному нефтепроводу напор, развиваемый насосами перекачивающих станций, расходуется на трение жидкости о стенку трубы h, преодоление местных сопротивлений hмс, статического сопротивления из-за разности геодезических (нивелирных) отметок z, а также создания требуемого остаточного напора в конце трубопровода hост.
Полные потери напора в трубопроводе составят
H = h+ hмс + z + hост. (1.10)
потери напора на местные сопротивления составляют 1…3% от линейных потерь. Тогда выражение (1.10) примет вид
H = 1,02h+ z + hост. (1.11)
Остаточный напор hост необходим для преодоления сопротивления технологических коммуникаций и заполнения резервуаров конечного пункта Потери напора на трение в трубопроводе определяют по формуле Дарси-Вейсбаха
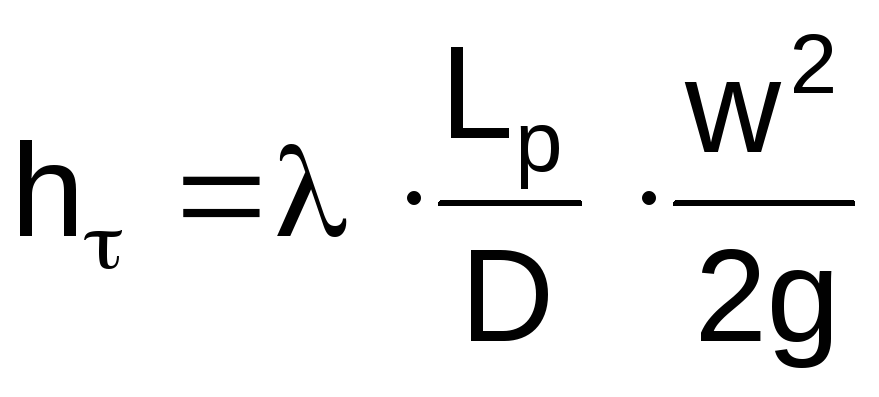 , (1.12)
, (1.12)
либо по обобщенной формуле лейбензона
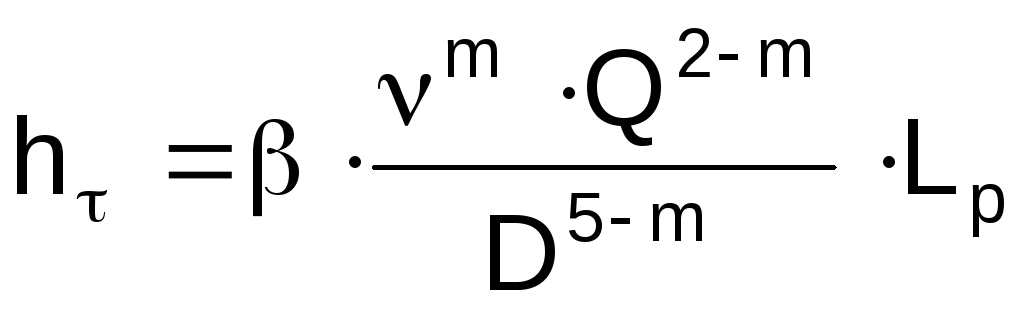 , (1.13)
, (1.13)
где Lр – расчетная длина нефтепровода;
w – средняя скорость течения нефти по трубопроводу;
– расчетная кинематическая вязкость нефти;
– коэффициент гидравлического сопротивления;
, m – коэффициенты обобщенной формулы Лейбензона.
Значения , и m зависят режима течения жидкости и шероховатостью внутренней поверхности трубы. Режим течения жидкости характеризуется безразмерным параметром Рейнольдса
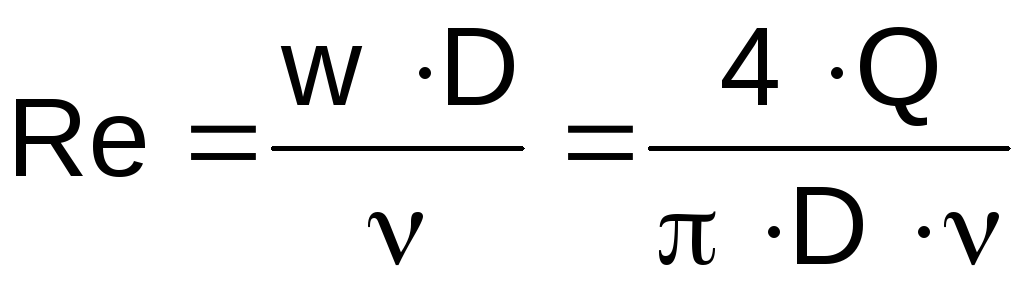 , (1.14)
, (1.14)
Гидравлический уклон
Гидравлическим уклоном называют потери напора на трение, отнесенные к единице длины трубопровода
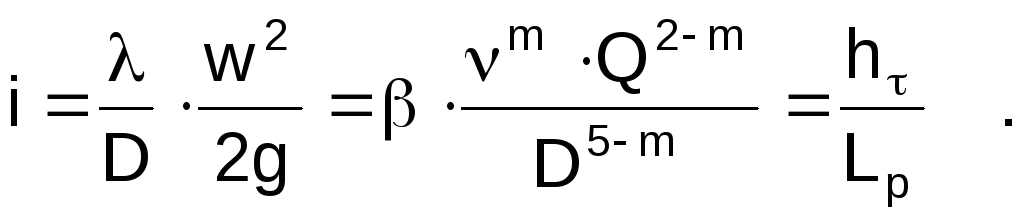 (1.15)
(1.15)
С учетом (1.15) уравнение (1.11) принимает вид
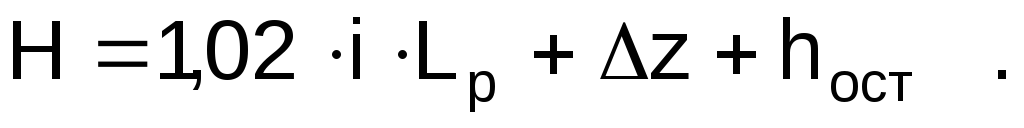 (1.16)
(1.16)
9 Определение перевальной точки и расчетной длины нефтепровода
Перевальной точкой называется такая возвышенность на трассе нефтепровода, от которой нефть приходит к конечному пункту нефтепровода самотеком. Таких вершин в общем случае может быть несколько. Расстояние от начала нефтепровода до ближайшей из них называется расчетной длиной нефтепровода. Рассмотрим это на примере нефтепровода протяженностью L, диаметром D и производительностью Q
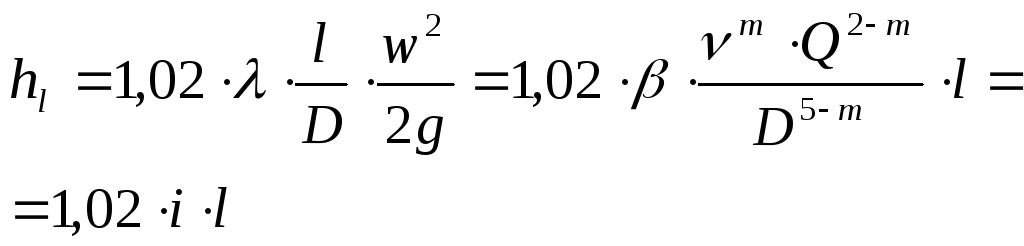 .
.
Соединив точки b и c, получим треугольник abc, называемый также гидравлическим треугольником. Его гипотенуза bc определяет положение линии гидравлического уклона в выбранных масштабах.
. Место касания линии 2 с линией профиля обозначает положение перевальной точки, определяющей расчетную длину нефтепровода.
Это говорит о том, что достаточно закачать нефть на перевальную точку, чтобы она с тем же расходом достигла конечного пункта трубопровода. Самотек нефти обеспечен, так как располагаемый напор (zПТ – zK – hОТ) больше напора, необходимого на преодоление сопротивления на участке от перевальной точки до конечного пункта
(zПТ – zK – hОТ)>i∙(L– lПТ) ,
где lПТ – расстояние от начального пункта нефтепровода до перевальной точки.
В этом случае за расчетную длину трубопровода принимают расстояние LP=lПТ, а разность геодезических отметок принимается равной z= zПТ – zH. Если пересечение линии гидравлического уклона с профилем отсутствует, то расчетная длина трубопровода равна его полной длине LP=L, а z= zK– zH.
1 0.Для
магистрального нефтепровода постоянного
диаметра с n
перекачивающими станциями, уравнение
баланса напоров имеет вид
0.Для
магистрального нефтепровода постоянного
диаметра с n
перекачивающими станциями, уравнение
баланса напоров имеет вид 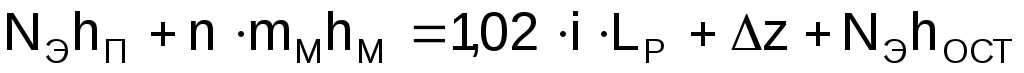 .
.
В начале каждого эксплуатационного участка ПС оснащены подпорными насосами. В конце трубопровода и каждого эксплуатационного участка требуется обеспечить остаточный напор hОСТ для преодоления сопротивления технологических трубопроводов и закачки в резервуары.
Правая часть уравнения (1.34) представляет собой полные потери напора в трубопроводе, то есть Н. В случае наличия вставок или лупингов по трассе правая часть уравнения (1.34) определяется по формуле (1.32).
Левая часть уравнения (1.34) – суммарный напор, развиваемый всеми работающими насосами перекачивающих станций (активный напор). С помощью коэффициентов характеристик насосов активный суммарный напор может быть представлен зависимостью
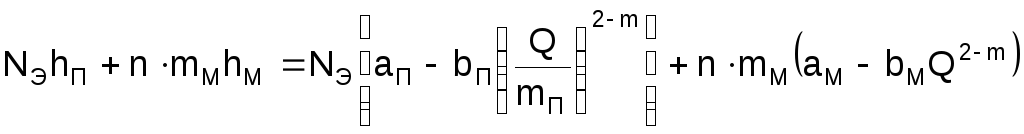 ,
,
аП, bП, hП – коэффициенты характеристики и напор, развиваемый подпорным насосом при подаче Q;
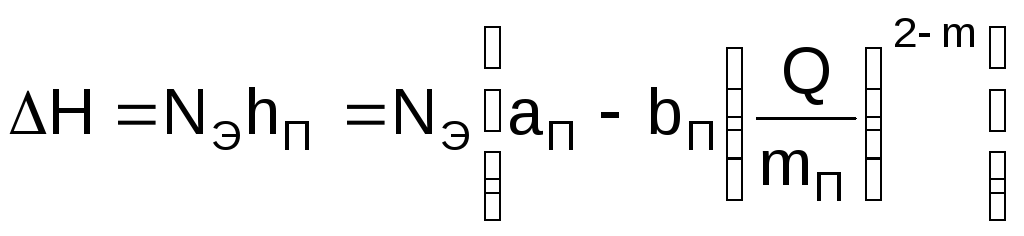 и
и
 ,
,
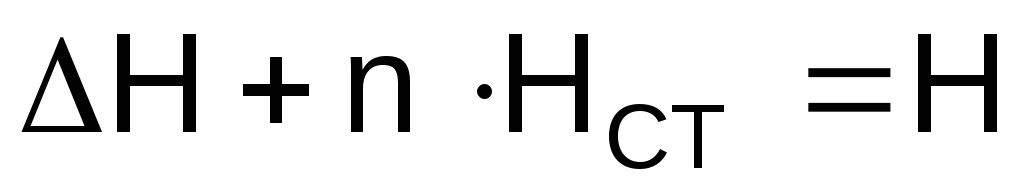 ,
(1.36)
,
(1.36)
Выразив левую часть уравнения (1.34) через (1.35), а правую часть – через (1.30), получим уравнение баланса напоров в аналитической форме

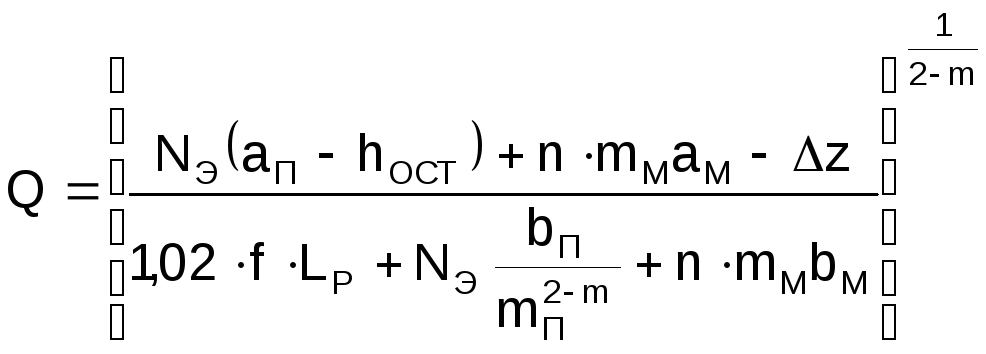 . (1.38)
. (1.38)
Если в общем случае на линейной части имеются лупинги и вставки, уравнение (1.38) примет вид
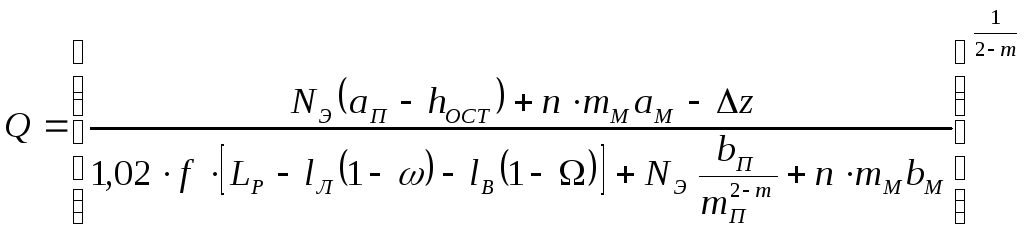 .
(1.39)
.
(1.39)
11.Точка пересечения характеристик называется рабочей точкой (А), которая характеризует потери напора в нефтепроводе и его пропускную способность при заданных условиях перекачки (рис. 1.12). Равенство создаваемого и затраченного напоров, а также равенство подачи насосов и расхода нефти в трубопроводе приводят к важному выводу: трубопровод и перекачивающие станции составляют единую гидравлическую систему. Изменение режима работы ПС (отключение части насосов или станций) приведет к изменению режима нефтепровода в целом. Изменение гидравлического сопротивления трубопровода или отдельного его перегона (изменение вязкости, включение резервных ниток, замена труб на отдельных участках трассы и т. п.) в свою очередь окажет влияние на режим работы всех перекачивающих станций.

1 – характеристика трубопровода;
2 – характеристика перекачивающих станций

5.2. Расчёт потерь давления в трубопроводах.
Потери давления
в трубопроводах (напорном
и сливном)
состоят
из
потерь
на
преодоление
гидравлических
сопротивления по
длине
∆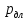 и
на преодоление потерь
в
местных
сопротивления
∆
и
на преодоление потерь
в
местных
сопротивления
∆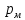 .
Соответственно
общепринятой
в гидравлике методикой
потери
по
длине для каждого участка трубопровода
определяются по формуле А. Дарси:
.
Соответственно
общепринятой
в гидравлике методикой
потери
по
длине для каждого участка трубопровода
определяются по формуле А. Дарси:
∆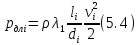
а местные — по формуле Вейсбаха
∆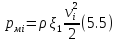
где  — длина,
диаметр и фактическая (определенная по
стандартному диаметру) скорость на
расчётных участках трубопровода;
— длина,
диаметр и фактическая (определенная по
стандартному диаметру) скорость на
расчётных участках трубопровода; 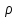 – плотность рабочей жидкости при
заданной температуре;
– плотность рабочей жидкости при
заданной температуре; 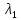 —
коэффициент гидравлического трения;
—
коэффициент гидравлического трения; 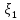 —
коэффициент местных сопротивлений.
—
коэффициент местных сопротивлений.
Для определения коэффициента гидравлического трения необходимо определить число Рейнольдса:
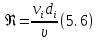
где 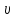 –
кинематическая вязкость рабочей жидкости
–
кинематическая вязкость рабочей жидкости
Для напорного трубопровода
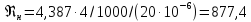
Для сливного трубопровода
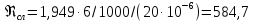
При
ламинарном режиме (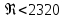 )
движения жидкости коэффициент
гидравлического трения для гибких
трубопроводов6
)
движения жидкости коэффициент
гидравлического трения для гибких
трубопроводов6
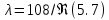
 0,123;
0,123; 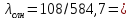 0,185.
0,185.
Потери давления по длине определяем для двух напорных и двух сливных линий согласно определенным в них скоростям
∆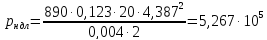 МПа
МПа
∆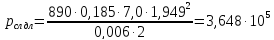 МПа
МПа
При
расчете потерь давления на преодоление
местных сопротивлений зависимостью 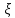 от Re
пренебрегают, принимая величину этого
коэффициента постоянной для каждого
конкретного типа местных сопротивлений.
Для штуцеров — 0,1,
прямоугольных тройников -1,
выхода из трубы в бак — 1,
входа в трубу — 0,5,
закругленное колено -0,12 … 0,15 (табл.
1.6 и Приложение 20 [1]).
от Re
пренебрегают, принимая величину этого
коэффициента постоянной для каждого
конкретного типа местных сопротивлений.
Для штуцеров — 0,1,
прямоугольных тройников -1,
выхода из трубы в бак — 1,
входа в трубу — 0,5,
закругленное колено -0,12 … 0,15 (табл.
1.6 и Приложение 20 [1]).
Тогда согласно участкам трубопроводов составим таблицы количества местных сопротивлений.
Для напорного трубопровода
Вид сопротивления | переходники | тройники слияния | тройники разделения | резкое уширение | резкое сужение | закругленное колено | колено без закругления | вход в трубу | вход в бак |
коэффициент сопротивления | 0,15 | 2 | 1 | 0,8 | 0,5 | 0,15 | 1 | 0,5 | 1 |
количество | 4 | 0 | 0 | 2 | 2 | 3 | 0 | 1 | 0 |
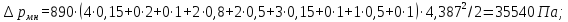
Для сливного трубопровода:
Вид сопротивления | переходники | тройники слияния | тройники разделения | резкое уширение | резкое сужение | закругленное колено | колено без закругления | вход в трубу | вход в бак |
коэффициент сопротивления | 0,15 | 2 | 1 | 0,8 | 0,5 | 0,15 | 1 | 0,5 | 1 |
количество | 1 | 0 | 0 | 2 | 2 | 5 | 0 | 0 | 1 |
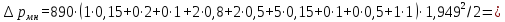 7607Па
7607Па
Для сливного трубопровода:
Вид сопротивления | переходники | тройники слияния | тройники разделения | резкое уширение | резкое сужение | закругленное колено | колено без закругления | вход в трубу | вход в бак |
коэффициент сопротивления | 0,15 | 2 | 1 | 0,8 | 0,5 | 0,15 | 1 | 0,5 | 1 |
количество | 0 | 0 | 0 | 2 | 2 | 3 | 0 | 0 | 1 |
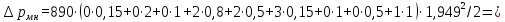 6846Па.
6846Па.
Суммарные потери давления в трубопроводах определяют по зависимости
 +
+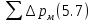
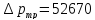 +
+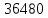 +7607+6846=0,104МПа
+7607+6846=0,104МПа
6. Определение давления насоса и его предварительный выбор
Давление насоса должно быть таким, чтобы была возможность обеспечить преодоление заданного полезного усилия исполняющего органа — гидроцилиндра, а также потерь давления на преодоление гидравлических сопротивлений в напорных и сливных трубопроводах и во всей гидравлической аппаратуре. Таким образом необходимое давление насоса будет равно:
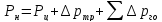 (6.1)
(6.1)
где 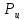 — рабочее давление в гидроцилиндре,
— рабочее давление в гидроцилиндре,  -потери
давления
на
преодоление
гидравлических
сопротивления
в
трубопроводах,
-потери
давления
на
преодоление
гидравлических
сопротивления
в
трубопроводах, 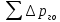 –
суммарные
потери
давления
в гидравлической аппаратуре,
которая находится
на напорной и сливной
линиях.
–
суммарные
потери
давления
в гидравлической аппаратуре,
которая находится
на напорной и сливной
линиях.
Учитывая
то, что для каждого гидроаппарата
потери
давления даны
в
технической
характеристике
для
максимального расхода,
необходимо
их пересчитать
на свой расход в системе, равный подаче
насоса 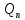 :
:
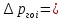 ∆
∆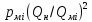 (6.2)
(6.2)
где
∆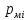 —
потери
давления при расходе
—
потери
давления при расходе .
При подсчете потерь давления в
фильтрах ∆
.
При подсчете потерь давления в
фильтрах ∆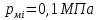 ,
а отношения
,
а отношения 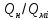 принимаются в первой степени.
принимаются в первой степени.
распределительное
устройство:  =0,15
=0,15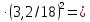 0,005МПа;
0,005МПа;
предохранительный
клапан 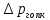 =0,2
=0,2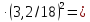 0,006МПа;
0,006МПа;
напорные
золотники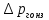 =0,4
=0,4 0,013МПа;
0,013МПа;
фильтр 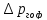 =0,1
=0,1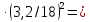 0,003МПа;
0,003МПа;
дроссель  =0,2
=0,2 0,006МПа
0,006МПа
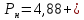 0,104+(0,005+0,006+0,013+0,003+0,006)=5,017МПа
0,104+(0,005+0,006+0,013+0,003+0,006)=5,017МПа
По
определенным значениям давления и
подачи по справочной литературе выбираем
из [2] табл.
4.5 пластинчатый насос Г12-21 с максимальным
рабочим давлением 6,3 Мпа, производительностью
0,2 л/с при n=24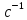 мощностью 2,20 кВт и объемным к.п.д.=0,71.
мощностью 2,20 кВт и объемным к.п.д.=0,71.
Потери напора на местные сопротивления
Местные
потери напора обусловливаются преодолением
местных сопротивлений, создаваемых
фасонными частями, арматурой и прочим
оборудованием трубопроводных сетей.
Местные сопротивления вызывают изменение
величины или направления скорости
движения жидкости на отдельных участках
трубопровода, что связано с появлением
дополнительных потерь напора. Движение
в трубопроводе при наличии местных
сопротивлений является неравномерным.
Потери напора в местных сопротивлениях  (местные
потери напора) вычисляют по формуле
Вейсбаха:
(местные
потери напора) вычисляют по формуле
Вейсбаха:
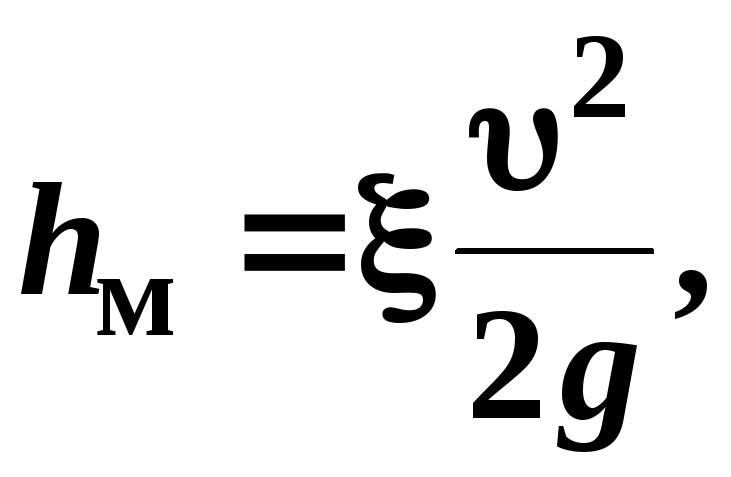 (3.22)
(3.22)
где  — средняя скорость в сечении, как
правило, расположенном ниже по течению
за данным сопротивлением;
— средняя скорость в сечении, как
правило, расположенном ниже по течению
за данным сопротивлением; — безразмерный
коэффициент местного сопротивления.
Для определения потерь давления
— безразмерный
коэффициент местного сопротивления.
Для определения потерь давления 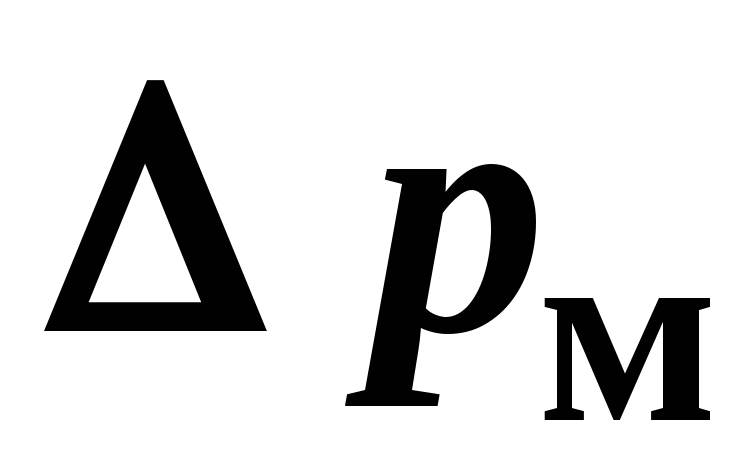 формула
(3.29) преобразуется к виду:
формула
(3.29) преобразуется к виду:
 (3.23)
(3.23)
Значения
коэффициентов местных сопротивлений
зависят от конфигурации местного
сопротивления и режима потока, подходящего
к сопротивлению; этот режим определяется
коэффициентом гидравлического трения  подходящего
потока, т.е. числом Рейнольдса и
относительной шероховатостью.
подходящего
потока, т.е. числом Рейнольдса и
относительной шероховатостью.
Внезапное расширение трубопровода
Рисунок 3.6 ─ Внезапное расширение трубопровода
Потери напора при внезапном расширении трубопровода находят по формуле Борда:
 (3.24)
(3.24)
где  и
и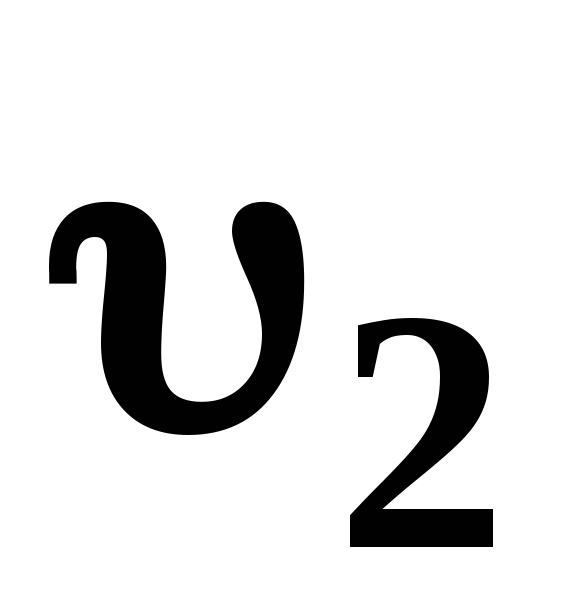 — средние скорости течения соответственно
до и после расширения.
— средние скорости течения соответственно
до и после расширения.
Таким образом, потеря напора при внезапном расширении трубопровода равна скоростному напору от потерянной скорости.
Коэффициент местного сопротивления в формуле Вейсбаха (3.29) определяется выражениями:
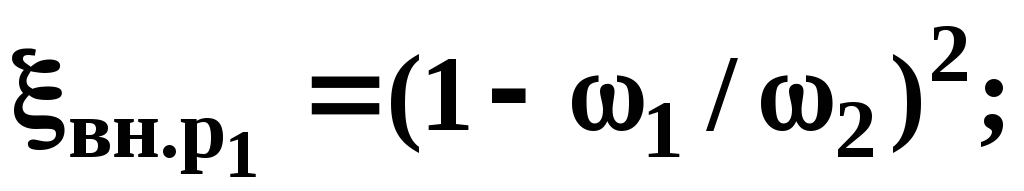 (3.25)
(3.25)
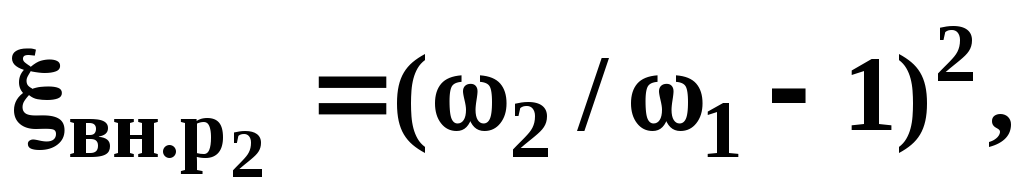 (3.26)
(3.26)
где  и
и — площади сечений трубопровода
соответственно до и после расширения.
— площади сечений трубопровода
соответственно до и после расширения.
Внезапное сужение трубопровода
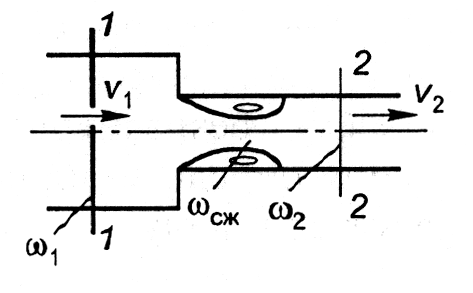
Рисунок 3.7 ─ Внезапное сужение трубопровода
Коэффициент местного сопротивления при внезапном сужении
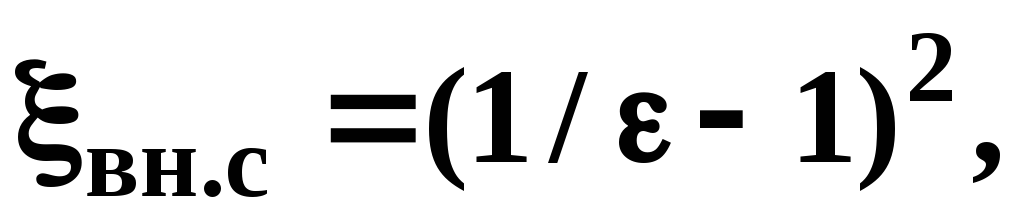 (3.27)
(3.27)
где  —
коэффициент сжатия струи, представляющий
собой отношение площади сечения сжатой
струи в узком трубопроводе
—
коэффициент сжатия струи, представляющий
собой отношение площади сечения сжатой
струи в узком трубопроводе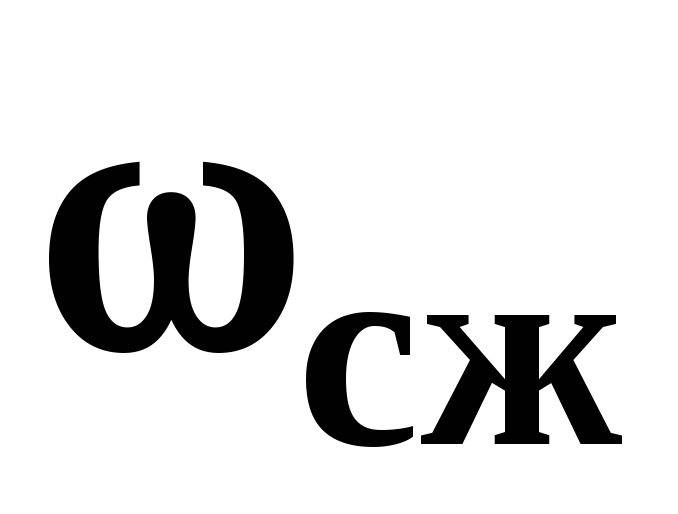 к площади сечения узкой трубы
к площади сечения узкой трубы (рисунок
3.9):
(рисунок
3.9):
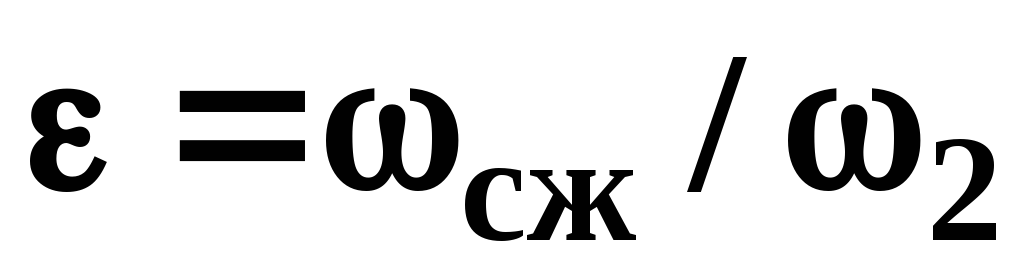 (3.28)
(3.28)
Коэффициент
сжатия струи  зависит от степени сжатия потока
зависит от степени сжатия потока
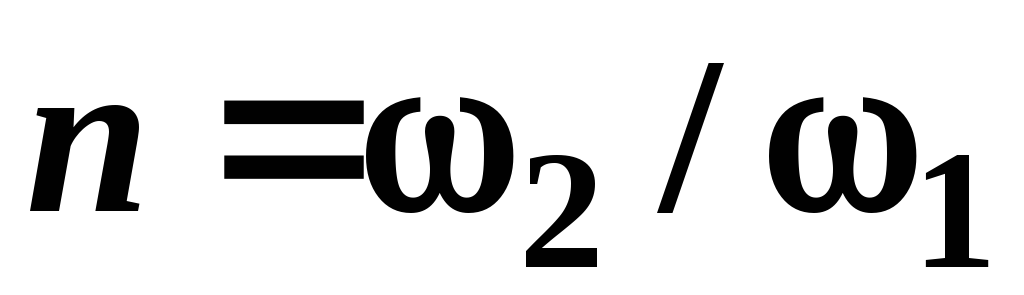 (3.29)
(3.29)
и может быть найден по формуле А.Д. Альтшуля:
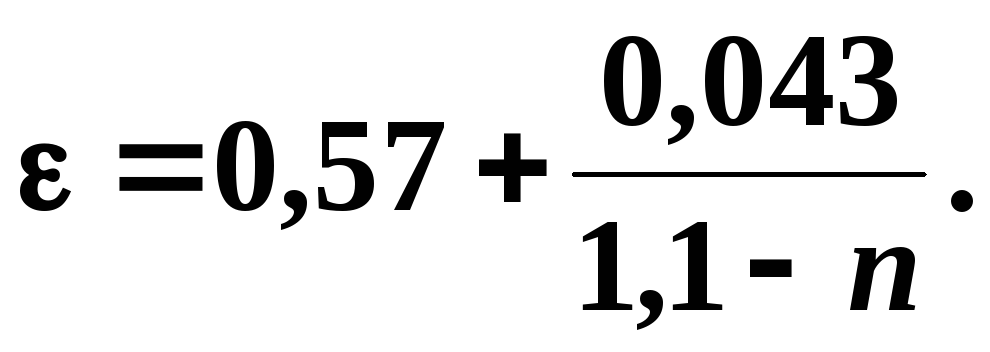 (3.30)
(3.30)
Значения  подсчитанные по формуле (3.30), приведены
в табл. 3.1
подсчитанные по формуле (3.30), приведены
в табл. 3.1
Таблица 3.1 ─ Коэффициент сжатия струи
| 0 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1 |
| 0,609 | 0,613 | 0,618 | 0,623 | 0,631 | 0,642 | 0,656 | 0,678 | 0,714 | 0,785 | 1 |
Диафрагма на трубопроводе
Рисунок 3.8 ─ Диафрагма на трубе постоянного сечения
Коэффициент местного сопротивления диафрагмы, расположенной внутри трубы постоянного сечения (отнесенный к сечению трубопровода) (рисунок 3.8) равен
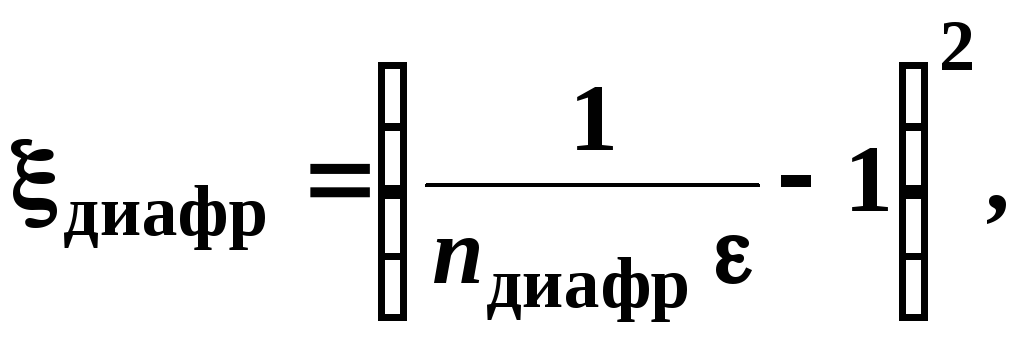 (3.31)
(3.31)
где 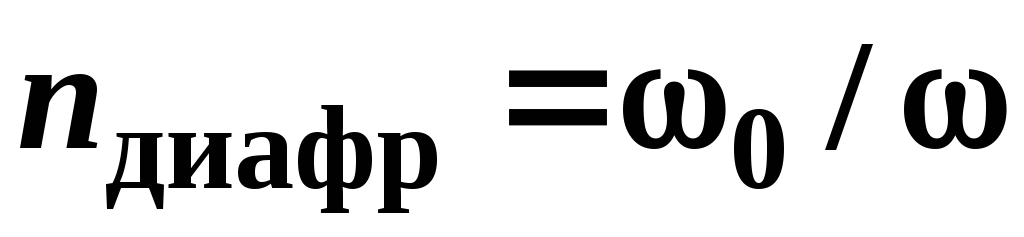 — отношение площади отверстия диафрагмы
— отношение площади отверстия диафрагмы к площади сечения трубы
к площади сечения трубы .
.
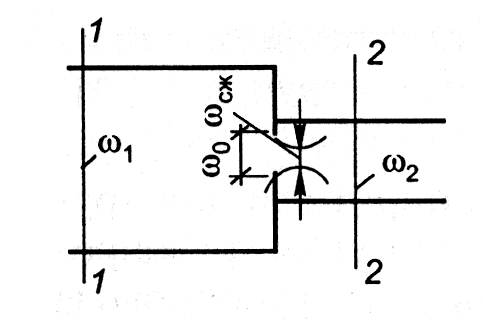
Рисунок 3.9 ─ Диафрагма на трубопроводе в месте изменения
диаметра
Коэффициент местного сопротивления (отнесенный к сечению узкого трубопровода) для диафрагмы, расположенной на выходе в трубопровод другого диаметра (рисунок 3.9), равен
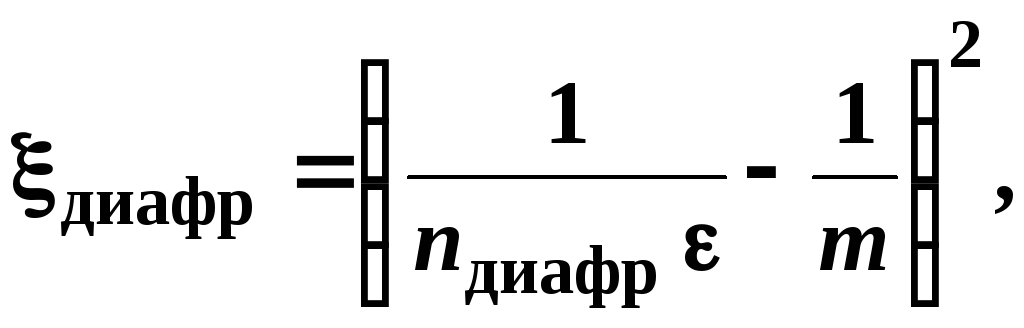 (3.32)
(3.32)
где 
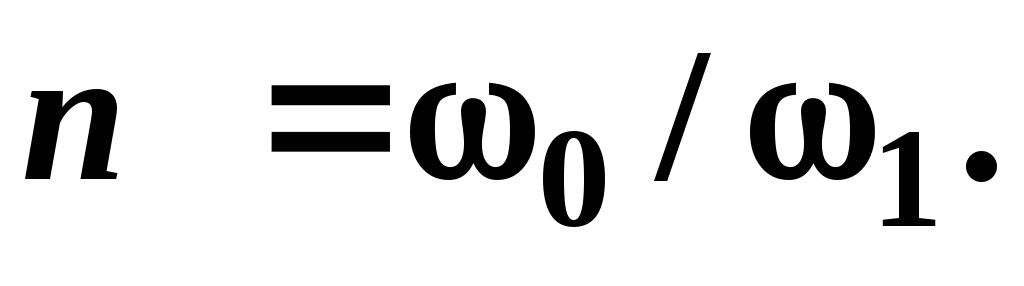
Задача №1. Расчет коротких трубопроводов.
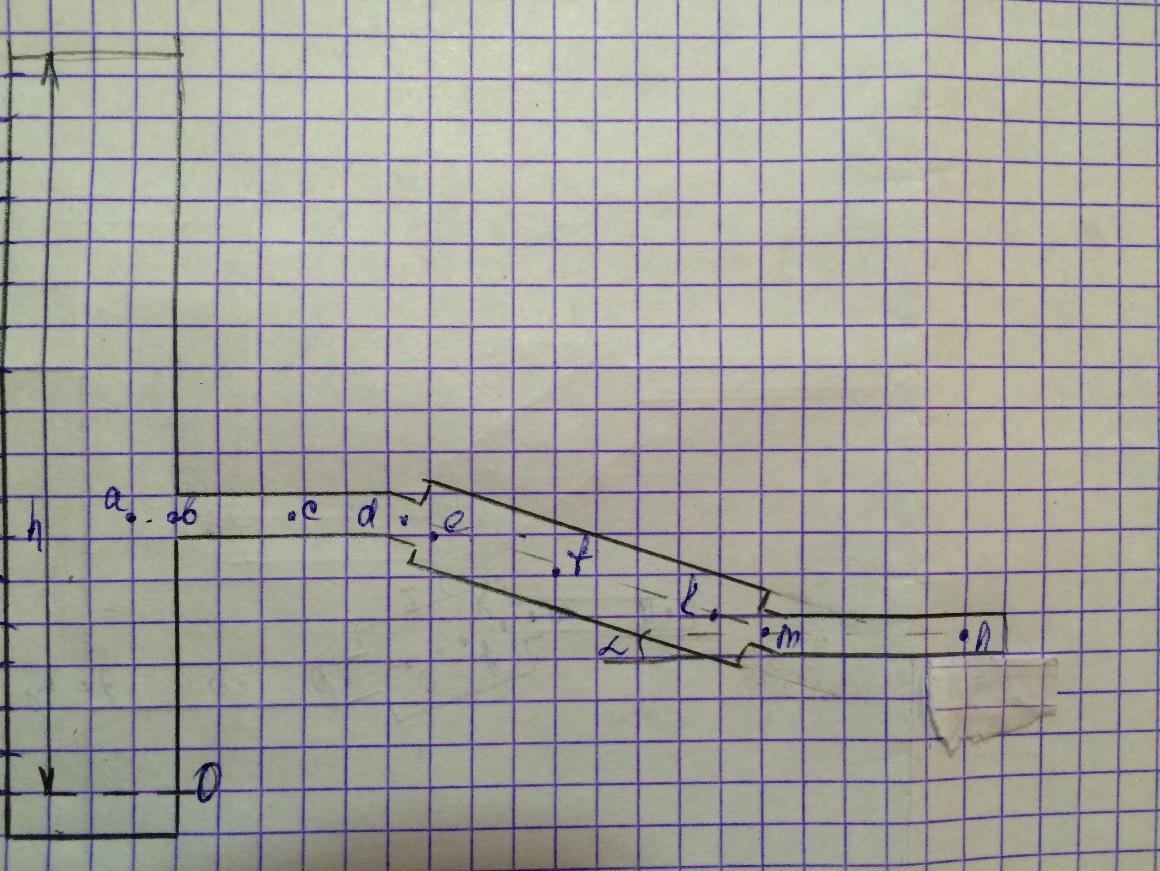 Рис.1.
Схема расположения трубопроводов.
Рис.1.
Схема расположения трубопроводов.
При расчете коротких трубопроводов применяется уравнение Бернулли для двух выбранных сечений и уравнение неразрывности.
Уравнение Бернулли составляется относительно плоскости сравнения, которой может быть любая горизонтальная плоскость. Плоскость сравнения проведена по центру трубы в начале трубопровода.
Расчет необходимо начать с определения формы записи уравнения Бернулли. Для расчета систем водоснабжения и водоотведения обычно применяется уравнение Бернулли в форме напоров:
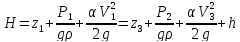 ,
,
где
высота z
называется геометрической высотой, или
высотой положения центра тяжести сечения
струйки; 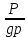 – высота, определяемая величиной
гидродинамического давления, или
пьезометрическая высота;
– высота, определяемая величиной
гидродинамического давления, или
пьезометрическая высота;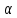 — коэффициент
— коэффициент
Кориолиса;  – скоростная высота, или скоростной
напор;
– скоростная высота, или скоростной
напор;  — потери напора.
— потери напора.
Если трубопровод имеет участки с разными диаметрами, то потери напора h при движении жидкости от сечения 1-1 к сечению 3-3 складываются из потерь во всех участках трубопровода. В каждом участке потери разделяются на потери по длине и местные.
1. Скорости потоков в трубах
Скорость потоков в трубах:
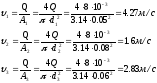
2. Расчёт потерь напора в трубопроводах
Потери
на выходе потока из бака определяется
по формуле
Вейсбаха: 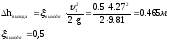
ζвыхода – коэффициент местного сопротивления
Потери напора по длине рассчитываются по формуле Дарси-Вейсбаха (труба 1):
Для определения потерь напора по длине трубы рассчитаем число Рейнольдса, по рассчитанному числу узнаем режим движения жидкости для всех участков с различными средними скоростями движения жидкости. Коэффициент гидравлического трения λ определяется по формулам, которые выбираются в зависимости от режима движения и области сопротивления.
Найдём число Рейнольдса

Число Рейнольдса определяет характер потока: ламинарный, промежуточный или турбулентный.
ламинарный , если Re <2300
промежуточный, если 2300 < Re <4000
турбулентный, если 4000 < Re
Зависимость коэффициента гидравлического сопротивления от числа Рейнольдса и эквивалентной шероховатости труб
Режим (зона) | Границы | Коэффициент гидравлического трения | |
Ламинарный | Re<2320 | | |
Турбулентный: | |||
1. | Зона перехода турбулентного движения в ламинарное | 2000<Re<3000 | |
2. | Зона гидравлически гладких труб | 2320<Re<10d/kэ | |
3. | Зона смешанного трения или гидравлически шероховатых труб | 10d/kэ<Re<500d/kэ | |
4. | Зона квадратичного сопротивления (вполне шероховатого трения) | Re>500d/kэ | |
Режим
движения жидкости турбулентный, так
как Re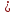 4000. Трубопровод гидравлически шероховатый,
1—
коэффициент гидравлического трения
рассчитывается по формуле Шифринсона:
4000. Трубопровод гидравлически шероховатый,
1—
коэффициент гидравлического трения
рассчитывается по формуле Шифринсона:
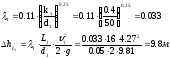
Потери напора на повороте:
ζпов.1 = ζ90° (1-cos20°)=0.06 м
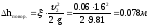
Потери напора при внезапном расширении рассчитывается по формуле Борда:
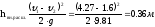
Потеря напора по длине (труба 2):
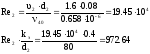
Режим
движения жидкости турбулентный, так
как Re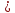 2320.
2320.
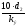
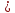 Re
Re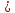
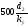 ;
4000 < 194529 < 200000
;
4000 < 194529 < 200000
Трубопровод гидравлически шероховатый.
Рассчитаем потери напора при внезапном сжатии:
n — коэффициент сжатия потока
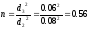
Коэффициент сужения струи находим по формуле Альтшуля:
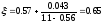
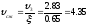
Потерю напора при внезапном сжатии находим по формуле Борда:
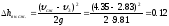
Потери напора на повороте:
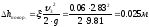
Потери напора по длине (труба 3):
Найдем число Рейнольдса:

Режим
движения жидкости турбулентный, так
как Re 2320. Трубопровод гидравлически шероховатый,
3—
коэффициент гидравлического трения
рассчитывается по формуле Альтшуля.
Потери
напора по длине рассчитываются по
формуле Дарси-Вейсбаха.
2320. Трубопровод гидравлически шероховатый,
3—
коэффициент гидравлического трения
рассчитывается по формуле Альтшуля.
Потери
напора по длине рассчитываются по
формуле Дарси-Вейсбаха.
Рассчитаем суммарные потери напора:
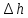 =
= 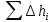 = 0,465+9,8+0,36+0,0078+0,0047+0,025+0,12+2,53=13,31м
= 0,465+9,8+0,36+0,0078+0,0047+0,025+0,12+2,53=13,31м
Местные потери напора — Водоснабжение, Водоотведение, Гидравлика
На этой странице собрана информация по коэффициентам местного сопротивления, которые могут быть использованы для расчета местных потерь напора в задачах инженерной практики
Задвижка

При расчете трубопроводных систем коэффициент сопротивления открытой задвижки принимается ζзадв = 0,1 — 0,2. Если задвижка прикрыта на определенную величину, то коэффициент сопротивления напрямую зависит от степени закрытия. Ниже представлена таблица зависимости коэффициента сопротивления задвижки от степени закрытия. Чем больше степень закрытия — тем больше коэффициент сопротивления.

| Степень закрытия (d-h)/d | 1/8 | 2/8 | 3/8 | 1/2 | 5/8 | 3/4 | 7/8 |
| ζзадв | 0,07 | 0,26 | 0,81 | 2,06 | 5,52 | 17,0 | 97,8 |
Шаровой кран

Коэффициент сопротивления шарового крана зависит от его диаметра (условного прохода). Ниже представлена таблица с коэффициентами. Диаметр крана приведен в дюймах (т.к. чаще всего он соединяется с трубами на резьбе), но ниже дан соответствующий диаметр в мм
| D, дюймы | 1/2 | 3/4 | 1 | 1 1/4 | 1 1/2 | 2 |
| D, мм | 15 | 20 | 25 | 32 | 40 | 50 |
| ζ | 0,26 | 0,13 | 0,12 | 0,11 | 0,103 | 0,101 |
По правилам русского языка, в отношении, в данном случае, запорной арматуры, элементом которой является шар, правильное произношение и написание будет шаровой кран, а не шаровый кран. Шаровый означает цвет (дымчато-серый)
Википедия
Вентиль

Коэффициент местного сопротивления вентиля для расчетов может быть принят равным 6
ζвент = 6
Поворотный затвор

Коэффициент сопротивления поворотного затвора для технических расчетов может быть принят равным 0,15 — 0,25
.
Обратный клапан

Коэффициент сопротивления обратного клапана для технических расчетов может быть принят равным 1,7
.
Плавный поворот

Коэффициент сопротивления при плавном повороте потока зависит от угла поворота ( α ) . Для стандартных отводов на 90о коэффициент ζ = 0,5 — 0,6. Коэффициент сопротивления при повороте на произвольный угол ( α ) может быть найден по формуле: ζпов = ζ90·α/90
Резкий поворот

Коэффициент местного сопротивления при резком повороте зависит от угла поворота ( α ). Эта зависимость представлена в табличной форме ниже
| α | 0 | 20 | 30 | 45 | 60 | 75 | 90 | 110 | 130 | 150 | 180 |
| ζпов | 0 | 0,13 | 0,16 | 0,32 | 0,56 | 0,81 | 1,19 | 1,87 | 2,59 | 3,20 | 3,60 |
Внезапное расширение

Потеря напора может быть рассчитана по скорости до (v₁) или после изменения диаметра (v₂)

Внезапное сужение

Потеря напора на внезапное сужение может быть также рассчитана по скорости (v₂) после сужения по формуле ниже:

Плавное расширение (переход расширяющийся)

Коэффициент местного сопротивления для стандартного расширяющегося перехода может быть принят ζпер.расш. = 0,25
! При вычислении потери напора скорость берется по меньшему диаметру !
.
Плавное сужение (переход сужающийся)

Коэффициент местного сопротивления для стандартного сужающегося перехода может быть принят ζпер.суж. = 0,1
При вычислении потери напора скорость также берется по меньшему диаметру
Обратный клапан с сеткой

При вычислении потерь напора на обратном клапане с сеткой, который устанавливается в определенных случаях на всасывающем трубопроводе от насоса для забора воды из водных объектов, коэффициент местного сопротивления может быть принят: ζобр.кл = 5,0 – 10,0
.
Вход в трубу

а) ζвх = 0,5
б) ζвх = 0,2
в) ζвх = 0,15
г) ζвх = 0,5 — 1,0
Коэффициент местного сопротивления при входе в трубу из резервуара зависит от того, как «оформлено» место входа. Скругленные кромки (вариант Б) уменьшают гидравлическое сопротивление. Если труба заведена вовнутрь (вариант Г), то коэффициент сопротивления, напротив, больше.
Вход в трубу с поворотом

Коэффициент сопротивления при входе в трубу из резервуара ζвх.α также зависит от угла поворота α. Чем больше угол — тем больше местное сопротивление.
| α | 90 | 75 | 60 | 45 |
| ζвх.α | 0,50 | 0,59 | 0,70 | 0,81 |
Выход в резервуар под уровень жидкости

Потери напора при выходе из трубопровода в резервуар под уровень жидкости равняются скоростному напору потока в месте выхода, т.е. коэффициент сопротивления ζвых = 1
.
Потери, связанные с течением жидкости через тройники




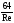 (формула
Стокса)
(формула
Стокса)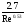 (формула
Френкеля)
(формула
Френкеля)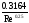 (формула
Блазиуса)
(формула
Блазиуса) (формула
Конакова при Re<3*106)
(формула
Конакова при Re<3*106)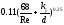 (формула
Альтшуля)
(формула
Альтшуля)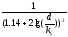 (формула
Никурадзе)
(формула
Никурадзе)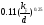 (формула
Шифринсона)
(формула
Шифринсона)