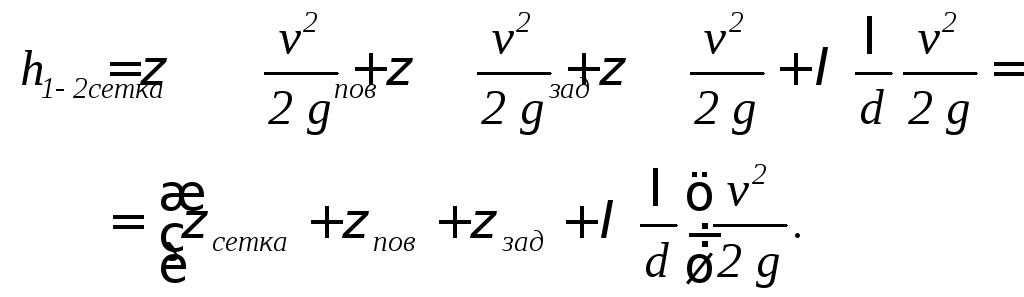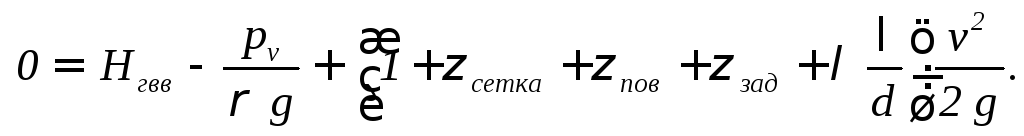Гидравлический расчёт трубопроводов » СтудИзба
5 ГИДРАВЛИЧЕСКИЙ РАСЧЕТ ТРУБОПРОВОДОВ
5.1 Простой трубопровод постоянного сечения
Трубопровод называется простым, если он не имеет ответвлений. Простые трубопроводы могут образовывать соединения: последовательное, параллельное или разветвленное. Трубопроводы могут быть сложными, содержащими как последовательное, так и параллельное соединения или разветвления.
Жидкость движется по трубопроводу благодаря тому, что ее энергия в начале трубопровода больше, чем в конце. Этот перепад (разность) уровней энергии может быть создан тем или иным способом: работой насоса, благодаря разности уровней жидкости, давлением газа. В машиностроении приходится иметь дело главным образом с трубопроводами, движение жидкости в которых обусловлено работой насоса.
При гидравлическом расчете трубопровода чаще всего определяется его потребный напор Hпотр — величина, численно равная пьезометрической высоте в начальном сечении трубопровода. Если потребный напор задан, то его принято называть располагаемым напором Hрасп. В этом случае при гидравлическом расчете может определяться расход Q жидкости в трубопроводе или его диаметр d. Значение диаметра трубопровода выбирается из установленного ряда в соответствии с ГОСТ 16516—80.
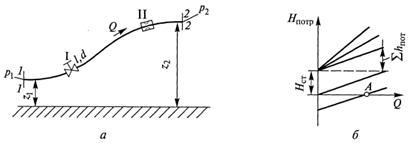
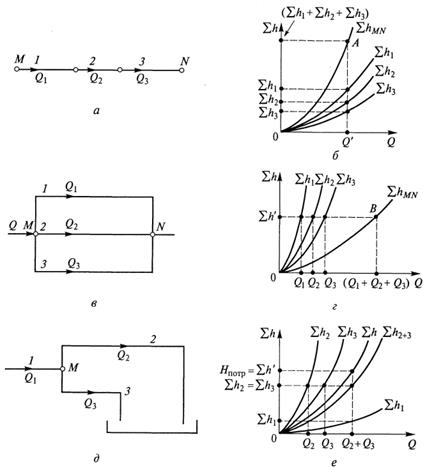
Пусть простой трубопровод постоянного проходного сечения, произвольно расположенный в пространстве (рисунок 5.1, а), имеет общую длину l и диаметр d и содержит ряд местных гидравлических сопротивлений I и II.
Запишем уравнение Бернулли для начального 1-1 и конечного 2-2 сечений этого трубопровода, считая, что коэффициенты Кориолиса в этих сечениях одинаковы (α1=α2). После сокращения скоростных напоров получим
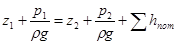 ,
,
где z1, z2 — координаты центров тяжести соответственно начального и конечного сечений;
p1, p2 — давления в соответственно начальном и конечном сечениях трубопровода;
 — суммарные потери напора в трубопроводе.
— суммарные потери напора в трубопроводе.
Отсюда потребный напор
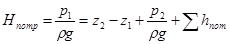 , (5.1)
, (5.1)
Как видно из полученной формулы, потребный напор складывается из суммарной геометрической высоты Δz = z2 – z1, на которую поднимается жидкость в процессе движения по трубопроводу, пьезометрической высоты в конечном сечении трубопровода и суммы гидравлических потерь напора, возникающих при движении жидкости в нем.
В гидравлике принято под статическим напором трубопровода понимать сумму 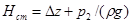 .
.
|

Тогда, представляя суммарные потери 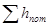 как степенную функцию от расхода Q, получим
как степенную функцию от расхода Q, получим
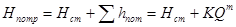 , (5.2)
, (5.2)
где т — величина, зависящая от режима течения жидкости в трубопроводе;
К — сопротивление трубопровода.
При ламинарном режиме течения жидкости и линейных местных сопротивлениях (заданы их эквивалентные длины lэкв) суммарные потери
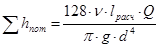 ,
,
где lрасч = l + lэкв — расчетная длина трубопровода.
Следовательно, при ламинарном режиме т = 1, 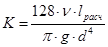 .
.
При турбулентном течении жидкости
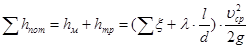 .
.
Заменяя в этой формуле среднюю скорость жидкости через расход, получим суммарные потери напора
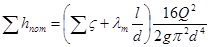 . (5.3)
. (5.3)
Тогда при турбулентном режиме 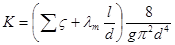 , а показатель степени m = 2. При этом следует помнить, что в общем случае коэффициент потерь на трение по длине
, а показатель степени m = 2. При этом следует помнить, что в общем случае коэффициент потерь на трение по длине 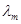 является также функцией расхода Q.
является также функцией расхода Q.
Поступая аналогично в каждом конкретном случае, после несложных алгебраических преобразований и вычислений можно получить формулу, определяющую аналитическую зависимость потребного напора для данного простого трубопровода от расхода в нем. Примеры таких зависимостей в графическом виде приведены на рисунке 5.1, б, в.
Анализ формул, приведенных выше, показывает, что решение задачи по определению потребного напора Hпотр при известных расходе Q жидкости в трубопроводе и его диаметре d несложно, так как всегда можно провести оценку режима течения жидкости в трубопроводе, сравнивая критическое значение Reкp = 2300 с его фактическим значением, которое для труб круглого сечения может быть вычислено по формуле
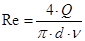 . (5.4)
. (5.4)
После определения режима течения можно вычислить потери напора, а затем потребный напор по формуле (5.2).
Если же величины Q или d неизвестны, то в большинстве случаев сложно оценить режим течения, а, следовательно, обоснованно выбрать формулы, определяющие потери напора в трубопроводе. В такой ситуации можно рекомендовать использовать либо метод последовательного приближения, обычно требующий достаточно большого объема вычислительной работы, либо графический метод, при применении которого необходимо строить так называемую характеристику потребного напора трубопровода.
5.2. Построение характеристики потребного напора простого трубопровода
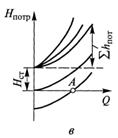
Графическое представление в координатах Н—Q аналитической зависимости (5.2), полученной для данного трубопровода, в гидравлике называется характеристикой потребного напора. На рисунке 5.1, б, в приведено несколько возможных характеристик потребного напора (линейные — при ламинарном режиме течения и линейных местных сопротивлениях; криволинейные — при турбулентном режиме течения или наличии в трубопроводе квадратичных местных сопротивлений).
Как видно на графиках, значение статического напора Нст может быть как положительным (жидкость подается на некоторую высоту Δz или в конечном сечении существует избыточное давление p2), так и отрицательным (при течении жидкости вниз или при ее движении в полость с разрежением).
Крутизна характеристик потребного напора зависит от сопротивления трубопровода и возрастает с увеличением длины трубы и уменьшением ее диаметра, а также зависит от количества и характеристик местных гидравлических сопротивлений. Кроме того, при ламинарном режиме течения рассматриваемая величина пропорциональна еще и вязкости жидкости. Точка пересечения характеристики потребного напора с осью абсцисс (точка А на рисунке 5.1, б, в) определяет расход жидкости в трубопроводе при движении самотеком.
Графические зависимости потребного напора широко используются для определения расхода Q при расчете как простых трубопроводов, так и сложных. Поэтому рассмотрим методику построения такой зависимости (рисунок 5.2, а). Она состоит из следующих этапов.
1-й этап. Используя формулу (5.4) определяем значение критического расхода Qкр, соответствующее Reкp=2300, и отмечаем его на оси расходов (ось абсцисс). Очевидно, что для всех расходов, расположенных левее Qкр, в трубопроводе будет ламинарный режим течения, а для расходов, расположенных правее Qкр, — турбулентный.
2-й этап. Рассчитываем значения потребного напора Н1и Н2при расходе в трубопроводе, равном Qкр, соответственно предполагая, что Н1 — результат расчета при ламинарном режиме течения, а Н2 — при турбулентном.
3-й этап. Строим характеристику потребного напора для ламинарного режима течения (для расходов, меньших Qкр). Если местные сопротивления, установленные в трубопроводе, имеют линейную зависимость потерь от расхода, то характеристика потребного напора имеет линейный вид.
4-й этап. Строим характеристику потребного напора для турбулентного режима течения (для расходов, больших Qкp). Во всех случаях получается криволинейная характеристика, близкая к параболе второй степени.
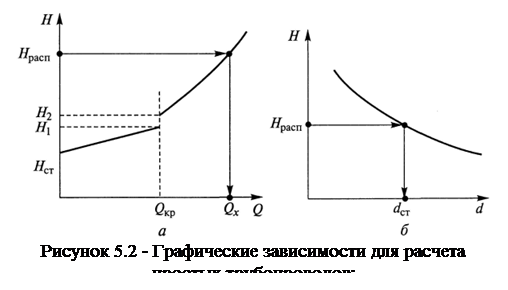
Имея характеристику потребного напора для данного трубопровода, можно по известному значению располагаемого напора Hрасп найти искомое значение расхода Qx (см. рисунок 5.2, а).
Если же необходимо найти внутренний диаметр трубопровода d, то, задаваясь несколькими значениями d, следует построить зависимость потребного напора Hпотр от диаметра d (рис. 5.2, б). Далее по значению Нраспвыбирается ближайший больший диаметр из стандартного ряда dст.
В ряде случаев на практике при расчете гидросистем вместо характеристики потребного напора используют характеристику трубопровода. Характеристика трубопровода — это зависимость суммарных потерь напора в трубопроводе от расхода. Аналитическое выражение этой зависимости имеет вид
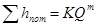 . (5.5)
. (5.5)
Сравнение формул (5.5) и (5.2) позволяет заключить, что характеристика трубопровода отличается от характеристики потребного напора отсутствием статического напора Hст, а при Hст = 0 эти две зависимости совпадают.
5.3 Соединения простых трубопроводов.
Аналитические и графические способы расчета
Рассмотрим способы расчета соединений простых трубопроводов.
Пусть имеем последовательное соединение нескольких простых трубопроводов (1, 2 и 3 на рисунке 5.3, а) различной длины, разного диаметра, с различным набором местных сопротивлений. Так как эти трубопроводы включены последовательно, то в каждом из них имеет место один и тот же расход жидкости Q. Суммарная потеря напора для всего соединения (между точками М и N) 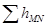 складывается из потерь напора в каждом простом трубопроводе (
складывается из потерь напора в каждом простом трубопроводе (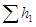 ,
, 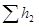 ,
, 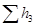 ), т.е. для последовательного соединения справедлива следующая система уравнений:
), т.е. для последовательного соединения справедлива следующая система уравнений:
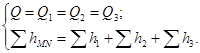 (5.6)
(5.6)
|

Потери напора в каждом простом трубопроводе могут быть определены через значения соответствующих расходов:
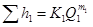 ;
; 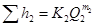 ;
; 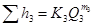 . (5.7)
. (5.7)
Система уравнений (5.6), дополненная зависимостями (5.7), является основой для аналитического расчета гидросистемы с последовательным соединением трубопроводов.
Если используется графический метод расчета, то при этом возникает необходимость в построении суммарной характеристики соединения.
На рисунке 5.3, б показан способ получения суммарной характеристики последовательного соединения. Для этого используются характеристики простых трубопроводов 1, 2 и 3, которые строятся по зависимостям (5.7).
Для построения точки, принадлежащей суммарной характеристике последовательного соединения, необходимо в соответствии с (5.6) сложить потери напора в исходных трубопроводах при одинаковом расходе. С этой целью на графике проводят произвольную вертикальную линию (при произвольном расходе Q‘). По этой вертикали суммируют отрезки (потери напора 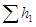 ,
, 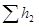 и
и  ) получившиеся от пересечения вертикали с исходными характеристиками трубопроводов. Полученная таким образом точка А будет принадлежать суммарной характеристике соединения. Следовательно, суммарная характеристика последовательного соединения нескольких простых трубопроводов получается в результате сложения ординат точек исходных характеристик при данном расходе.
) получившиеся от пересечения вертикали с исходными характеристиками трубопроводов. Полученная таким образом точка А будет принадлежать суммарной характеристике соединения. Следовательно, суммарная характеристика последовательного соединения нескольких простых трубопроводов получается в результате сложения ординат точек исходных характеристик при данном расходе.
Параллельным называется соединение трубопроводов, имеющих две общие точки (точку разветвления и точку смыкания). Пример параллельного соединения трех простых трубопроводов приведен на рисунке 5.3, в. Очевидно, что расход Q жидкости в гидросистеме до разветвления (точка М) и после смыкания (точка N) один и тот же и равен сумме расходов Q1, Q2 и Q3 в параллельных ветвях.
Если обозначить полные напоры в точках M и N через НM и HN, то для каждого трубопровода потеря напора равна разности этих напоров:
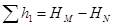 ;
; 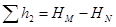 ;
; 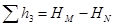 ,
,
т. е. в параллельных трубопроводах потери напора всегда одинаковы. Это объясняется тем, что при таком соединении, несмотря на разные гидравлические сопротивления каждого простого трубопровода, расходы Q1, Q2 и Q3 распределяются между ними так, что потери остаются равными.
Таким образом, система уравнений для параллельного соединения имеет вид
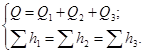 (5.8)
(5.8)
Потери напора в каждом трубопроводе, входящем в соединение, могут быть определены по формулам вида (5.7). Таким образом, система уравнений (5.8), дополненная формулами (5.7), является основой для аналитического расчета гидросистем с параллельным соединением трубопроводов.
На рисунке 5.3, г показан способ получения суммарной характеристики параллельного соединения. Для этого используются характеристики простых трубопроводов 1, 2 и 3, которые строятся по зависимостям (5.7).
Для получения точки, принадлежащей суммарной характеристике параллельного соединения, необходимо в соответствии с (5.8) сложить расходы в исходных трубопроводах при одинаковых потерях напора. С этой целью на графике проводят произвольную горизонтальную линию (при произвольной потере 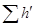 ). По этой горизонтали графически суммируют отрезки (расходы Q1, Q2 и Q3), получившиеся от пересечения горизонтали с исходными характеристиками трубопроводов. Полученная таким образом точка В принадлежит суммарной характеристике соединения. Следовательно, суммарная характеристика параллельного соединения трубопроводов получается в результате сложения абсцисс точек исходных характеристик при данных потерях.
). По этой горизонтали графически суммируют отрезки (расходы Q1, Q2 и Q3), получившиеся от пересечения горизонтали с исходными характеристиками трубопроводов. Полученная таким образом точка В принадлежит суммарной характеристике соединения. Следовательно, суммарная характеристика параллельного соединения трубопроводов получается в результате сложения абсцисс точек исходных характеристик при данных потерях.
По аналогичному методу строятся суммарные характеристики для разветвленных трубопроводов. Разветвленным соединением называется совокупность нескольких трубопроводов, имеющих одну общую точку (место разветвления или смыкания труб).
Рассмотренные выше последовательное и параллельное соединения, строго говоря, относятся к разряду сложных трубопроводов. Однако в гидравлике под сложным трубопроводом, как правило, понимают соединение нескольких последовательно и параллельно включенных простых трубопроводов.
На рисунке 5.3, д приведен пример такого сложного трубопровода, состоящего из трех трубопроводов 1, 2 и 3. Трубопровод 1 включен последовательно по отношению к трубопроводам 2 и 3. Трубопроводы 2 и 3 можно считать параллельными, так как они имеют общую точку разветвления (точка М) и подают жидкость в один и тот же гидробак.
Для сложных трубопроводов расчет, как правило, проводится графическим методом. При этом рекомендуется следующая последовательность:
1) сложный трубопровод разбивается на ряд простых трубопроводов;
2) для каждого простого трубопровода строится его характеристика;
3) графическим сложением получают характеристику сложного трубопровода.
На рисунке 5.3, е показана последовательность графических построений при получении суммарной характеристики (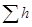 ) сложного трубопровода. Вначале складываются характеристики трубопроводов
) сложного трубопровода. Вначале складываются характеристики трубопроводов 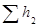 и
и  по правилу сложения характеристик параллельных трубопроводов, а затем характеристика
по правилу сложения характеристик параллельных трубопроводов, а затем характеристика 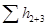 параллельного соединения складывается с характеристикой
параллельного соединения складывается с характеристикой 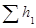 по правилу сложения характеристик последовательно соединенных трубопроводов и получается характеристика всего сложного трубопровода
по правилу сложения характеристик последовательно соединенных трубопроводов и получается характеристика всего сложного трубопровода 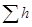 .
.
Имея построенный таким образом график (см. рисунок 5.3, е) для сложного трубопровода, можно достаточно просто по известному значению расхода Q1, поступающего в гидросистему, определить потребный напор Hпотр =  для всего сложного трубопровода, расходы Q2 и Q3 в параллельных ветвях, а также потери напора
для всего сложного трубопровода, расходы Q2 и Q3 в параллельных ветвях, а также потери напора 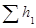 ,
, 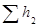 и
и 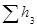 в каждом простом трубопроводе.
в каждом простом трубопроводе.
5.4 Трубопровод с насосной подачей
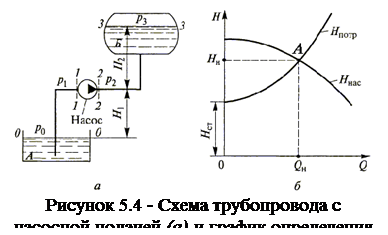
Как уже отмечалось, основным способом подачи жидкости в машиностроении является принудительное нагнетание ее насосом. Насосом называется гидравлическое устройство, преобразующее механическую энергию привода в энергию потока рабочей жидкости. В гидравлике трубопровод, в котором движение жидкости обеспечивается за счет насоса, называется трубопроводом с насосной подачей (рисунок 5.4, а).
Целью расчета трубопровода с насосной подачей, как правило, является определение напора, создаваемого насосом (напора насоса). Напором насоса Нн называется полная механическая энергия, переданная насосом единице веса жидкости. Таким образом, для определения Нн необходимо оценить приращение полной удельной энергии жидкости при прохождении ее через насос, т.е.
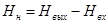 , (5.9)
, (5.9)
где Нвх, Нвых — удельная энергия жидкости соответственно на входе и выходе из насоса.
Рассмотрим работу разомкнутого трубопровода с насосной подачей (см. рисунок 5.4, а). Насос перекачивает жидкость из нижнего резервуара А с давлением над жидкостью p0 в другой резервуар Б, в котором давление р3. Высота расположения насоса относительно нижнего уровня жидкости H1 называется высотой всасывания, а трубопровод, по которому жидкость поступает к насосу, всасывающим трубопроводом, или гидролинией всасывания. Высота расположения конечного сечения трубопровода или верхнего уровня жидкости Н2 называется высотой нагнетания, а трубопровод, по которому жидкость движется от насоса, напорным, или гидролинией нагнетания.
 |
Запишем уравнение Бернулли для потока жидкости во всасывающем трубопроводе, т.е. для сечений 0-0 и 1-1:
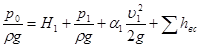 , (5.10)
, (5.10)
где 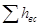 — потери напора во всасывающем трубопроводе.
— потери напора во всасывающем трубопроводе.
Уравнение (5.10) является основным для расчета всасывающих трубопроводов. Давление p0 обычно ограничено (чаще всего это атмосферное давление). Поэтому целью расчета всасывающего трубопровода, как правило, является определение давления перед насосом. Оно должно быть выше давления насыщенных паров жидкости. Это необходимо для исключения возникновения кавитации на входе в насос. Из уравнения (5.10) можно найти удельную энергию жидкости на входе в насос:
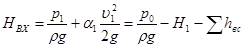 . (5.11)
. (5.11)
Запишем уравнение Бернулли для потока жидкости в напорном трубопроводе, т. е. для сечений 2-2 и 3-3:
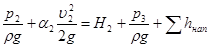 , (5.12)
, (5.12)
где 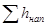 — потери напора в напорном трубопроводе.
— потери напора в напорном трубопроводе.
Левая часть этого уравнения представляет собой удельную энергию жидкости на выходе из насоса Hвых. Подставив в (5.9) правые части зависимостей (5.11) для Hвх и (5.12) для Hвых, получим
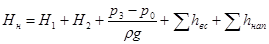 , (5.13)
, (5.13)
Как следует из уравнения (5.13), напор насоса Hн обеспечивает подъем жидкости на высоту (Н1+H2), повышение давления с р0 до p3 и расходуется на преодоление сопротивлений во всасывающем и напорном трубопроводах.
Если в правой части уравнения (5.13) 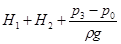 обозначить Hст и заменить
обозначить Hст и заменить 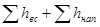 на KQm , то получим Hн=Hcr + KQm.
на KQm , то получим Hн=Hcr + KQm.
Сравним последнее выражение с формулой (5.2), определяющей потребный напор для трубопровода. Очевидна их полная идентичность:
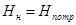 , (5.14)
, (5.14)
т.е. насос создает напор, равный потребному напору трубопровода.
Полученное уравнение (5.14) позволяет аналитически определить напор насоса. Однако в большинстве случаев аналитический способ достаточно сложен, поэтому получил распространение графический метод расчета трубопровода с насосной подачей.
Этот метод заключается в совместном построении на графике характеристики потребного напора трубопровода 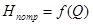 (или характеристики трубопровода
(или характеристики трубопровода 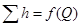 ) и характеристики насоса
) и характеристики насоса 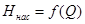 . Под характеристикой насоса понимают зависимость напора, создаваемого насосом, от расхода. Точка пересечения этих зависимостей называется рабочей точкой гидросистемы и является результатом графического решения уравнения (5.14).
. Под характеристикой насоса понимают зависимость напора, создаваемого насосом, от расхода. Точка пересечения этих зависимостей называется рабочей точкой гидросистемы и является результатом графического решения уравнения (5.14).
На рисунке 5.4, б приведен пример такого графического решения. Здесь точка А и есть искомая рабочая точка гидросистемы. Ее координаты определяют напор Hн, создаваемый насосом, и расход Qн жидкости, поступающей от насоса в гидросистему.
Если по каким-то причинам положение рабочей точки на графике не устраивает проектировщика, то это положение можно изменить, если скорректировать какие-либо параметры трубопровода или насоса.
7.5. Гидравлический удар в трубопроводе
Гидравлическим ударом называется колебательный процесс, возникающий в трубопроводе при внезапном изменении скорости жидкости, например при остановке потока из-за быстрого перекрытия задвижки (крана).
Этот процесс очень быстротечен и характеризуется чередованием резкого повышения и понижения давления, что может привести к разрушению гидросистемы. Это вызвано тем, что кинетическая энергия движущегося потока при остановке переходит в работу по растяжению стенок труб и сжатию жидкости. Наибольшую опасность представляет начальный скачок давления.
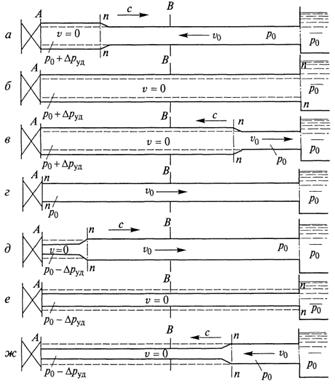
Проследим стадии гидравлического удара, возникающего в трубопроводе при быстром перекрытии потока (рисунок 7.5).
Пусть в конце трубы, по которой жидкость движется со скоростью vq, произведено мгновенное закрытие крана А. Тогда (см. рисунок 7.5, а) скорость частиц жидкости, натолкнувшихся на кран, будет погашена, а их кинетическая энергия перейдет в работу деформации стенок трубы и жидкости. При этом стенки трубы растягиваются, а жидкость сжимается. Давление в остановившейся жидкости возрастает на Δpуд. На заторможенные частицы жидкости у крана набегают другие частицы и тоже теряют скорость, в результате чего сечение п—п перемещается вправо со скоростью с, называемой скоростью ударной волны, сама же переходная область (сечение п—п), в которой давление изменяется на величину Δpуд, называется ударной волной.
Когда ударная волна достигнет резервуара, жидкость окажется остановленной и сжатой во всей трубе, а стенки трубы — растянутыми. Ударное повышение давления Δpуд распространится на всю трубу (см. рис. 7.5, б).
Но такое состояние не является равновесным. Под действием повышенного давления (р0 + Δpуд) частицы жидкости устремятся из трубы в резервуар, причем это движение начнется с сечения, непосредственно прилегающего к резервуару. Теперь сечение п—п перемещается по трубопроводу в обратном направлении — к крану — с той же скоростью с, оставляя за собой в жидкости давление p0 (см. рисунке 7.5, в).
|

Жидкость и стенки трубы возвращаются к начальному состоянию, соответствующему давлению p0. Работа деформации полностью переходит в кинетическую энергию, и жидкость в трубе приобретает первоначальную скорость 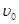 , но направленную в противоположную сторону.
, но направленную в противоположную сторону.
С этой скоростью «жидкая колонна» (см. рисунок 7.5, г) стремится оторваться от крана, в результате возникает отрицательная ударная волна (давление в жидкости уменьшается на то же значение Δpуд). Граница между двумя состояниями жидкости направляется от крана к резервуару со скоростью с, оставляя за собой сжавшиеся стенки трубы и расширившуюся жидкость (см. рисунок 7.5, д). Кинетическая энергия жидкости вновь переходит в работу деформации, но с противоположным знаком.
Состояние жидкости в трубе в момент прихода отрицательной ударной волны к резервуару показано на рисунке 7.5, е. Так же как и для случая, изображенного на рисунке 7.5, б, оно не является равновесным, так как жидкость в трубе находится под давлением (р0 + Δpуд), меньшим, чем в резервуаре. На рисунке 7.5, ж показан процесс выравнивания давления в трубе и резервуаре, сопровождающийся возникновением движения жидкости со скоростью 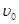 .
.
Очевидно, что как только отраженная от резервуара ударная волна достигнет крана, возникнет ситуация, уже имевшая место в момент закрытия крана. Весь цикл гидравлического удара повторится.
Теоретическое и экспериментальное исследования гидравлического удара в трубах было впервые выполнено Н.Е.Жуковским. В его опытах было зарегистрировано до 12 полных циклов с постепенным уменьшением Δpуд. В результате проведенных исследований Н.Е.Жуковский получил аналитические зависимости, позволяющие оценить ударное давление Δpуд. Одна из этих формул, получившая имя Н.Е.Жуковского, имеет вид
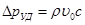 , (7.14)
, (7.14)
где скорость распространения ударной волны с определяется по формуле
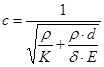 ,
,
где К — объемный модуль упругости жидкости; Е — модуль упругости материала стенки трубопровода; d и δ — соответственно внутренний диаметр и толщина стенки трубопровода.
Формула (7.14) справедлива при прямом гидравлическом ударе, когда время перекрытия потока tзакр меньше фазы гидравлического удара t0:
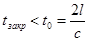 ,
,
где l — длина трубы.
Фаза гидравлического удара t0 — это время, за которое ударная волна движется от крана к резервуару и возвращается обратно. При tзакр > t0 ударное давление получается меньше, и такой гидроудар называют непрямым.
При необходимости можно использовать известные способы «смягчения» гидравлического удара. Наиболее эффективным из них является увеличение времени срабатывания кранов или других устройств, перекрывающих поток жидкости. Аналогичный эффект достигается установкой перед устройствами, перекрывающими поток жидкости, гидроаккумуляторов или предохранительных клапанов. Уменьшение скорости движения жидкости в трубопроводе за счет увеличения внутреннего диаметра труб при заданном расходе и уменьшение длины трубопроводов (уменьшение фазы гидравлического удара) также способствуют снижению ударного давления.
2.12. Основы расчета трубопроводов.
2.12.1. Типы трубопроводов и их классификация
В зависимости от величины местных потерь все трубопроводы делятся на гидравлически длинные и гидравлически короткие.
Трубопроводы, у которых основными являются потери по длине, а местными потерями можно пренебречь, называются гидравлически длинными трубопроводами (водопроводами).
Трубопроводы, у которых преобладают местные потери — короткими.
Простой трубопровод — из труб одного или двух диаметров и не имеет ответвлений.
Сложный трубопровод имеет магистраль с разветвлениями: разветвленные или тупиковые, замкнутые или кольцевые.
Расчет длинных трубопроводов:
— определить 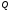 ,
при известных
,
при известных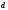
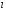 и
и 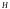 ;
; — определить 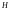 при известных,
при известных, 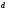 и l;
и l;
— определить 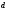 ,
при заданных
,
при заданных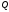
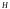 .
.Используется уравнение Бернулли:
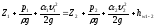 (110)
(110)
и уравнение постоянства расхода:
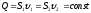 (111)
(111)
Уравнение Бернулли приводится к двум видам:
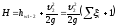 (112)
(112)
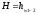 (113)
(113)Выражая расход через расходную характеристику К и гидравлический уклон I получим:
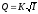 (114)
(114)
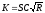 ,
(115)
,
(115)
где С — коэффициент потерь Шези;
R — гидравлический радиус, м.
для квадратичной области —
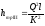 (116)
(116)
для Ι и ΙΙ зон —
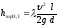 (117)
(117)
Коэффициенты
гидравлического трения 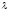 необходимо определить по формулам,
приведенным выше в зависимости от числа
Рейнольдса и относительной шероховатости
или по графику
необходимо определить по формулам,
приведенным выше в зависимости от числа
Рейнольдса и относительной шероховатости
или по графику
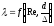 (118)
(118)
Правила выбора сечений:
сечения всегда выбираются перпендикулярно направлению движения жидкости;
сечение выбираются там, где известно максимальное число слагаемых уравнения Бернулли или там, где нужно что-то определить;
нумеровать сечения следует так, чтобы жидкость двигалась от 1 — 1 к 2 — 2.
2.12.3. Методика расчета простого трубопровода
Первый случай:
Имеем
простой трубопровод с постоянным
диаметром 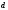
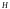 (рис. 43).
(рис. 43).Для сечений 1 — 1 и 2 — 2 напишем уравнение Бернулли:
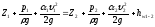 .
.
Так как 
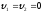 ,
давление
,
давление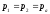
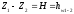 (119)
(119)
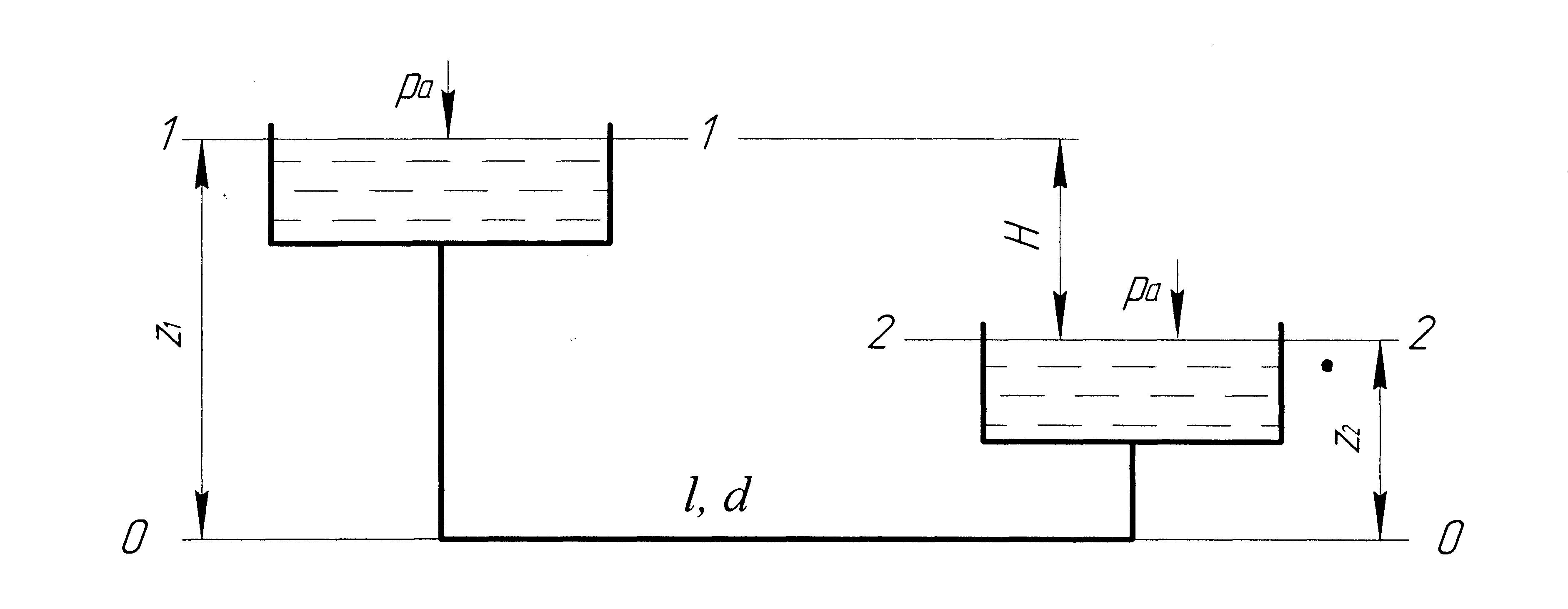

Рис. 43. Схема расчета прямого трубопровода (случай первый)
Так как мы имеем гидравлически длинный трубопровод, то пренебрегая местным сопротивлением, получим
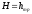 (120)
(120)
где  и
и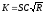 .
.
С учетом местных потерь
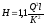 (121)
(121)
Второй случай:
Трубопровод состоит из последовательно соединенных труб разных диаметров (рис. 44).
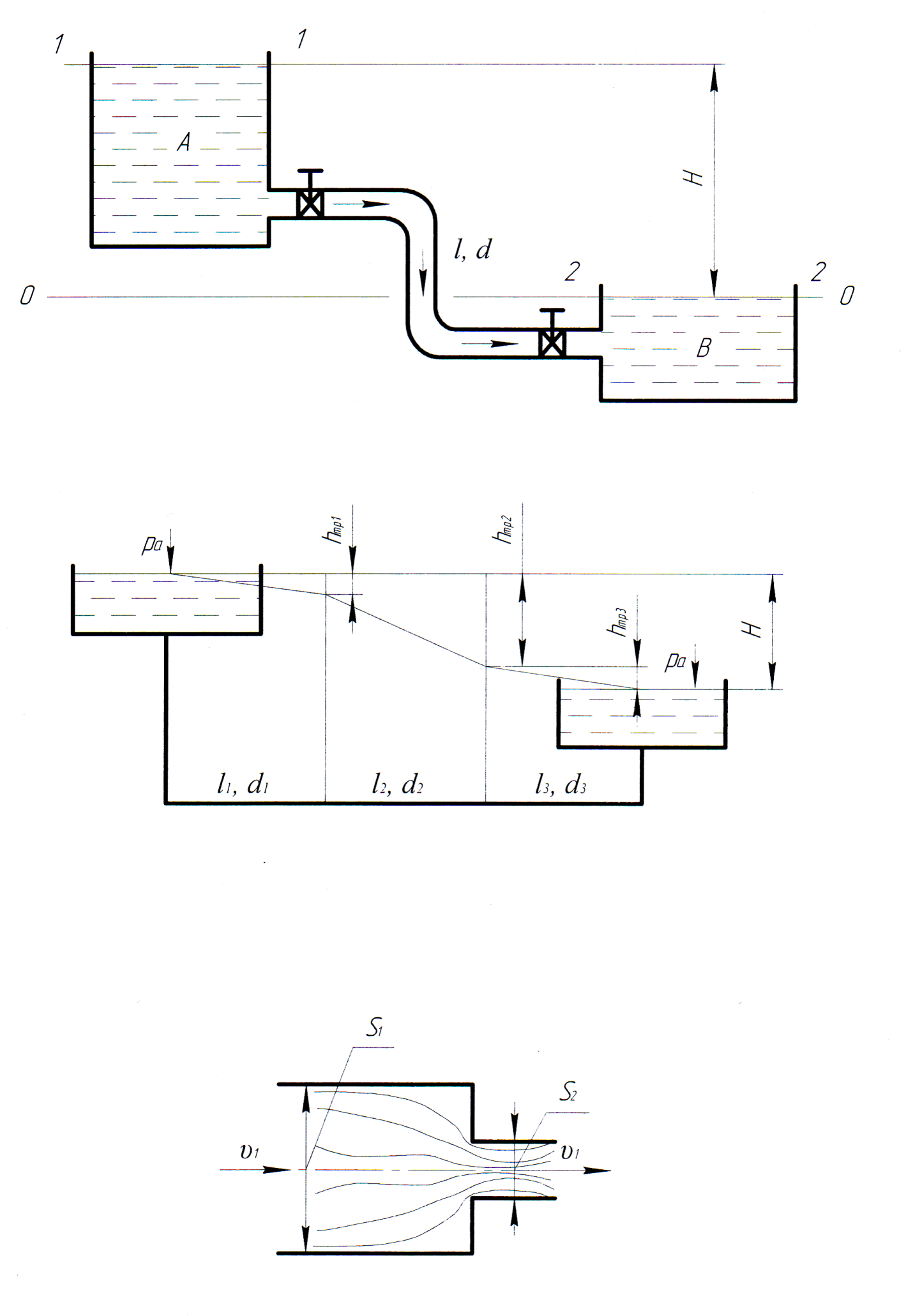
Рис. 44. Схема расчета простого трубопровода (случай второй)
Три участка длиной 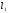 ,
, ,
,  с равными диаметрами труб
с равными диаметрами труб 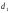 ,
, 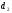 ,
, 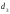
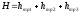 (122)
(122)
Потери на любом участке определим по формуле:
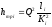 (123)
(123)
тогда 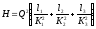 (144)
(144)
или  (145)
(145)
2.12.3. Расчет гидравлически коротких трубопроводов
Истечение жидкости под уровень (рис. 45).
Рис. 45. Схема расчета короткого трубопровода (случай первый)
Жидкость перетекает
из А в В.
Длина трубы 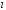 ,
диаметр
,
диаметр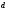 ,
разность уровней
,
разность уровней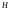 .
Движение — установившееся.
.
Движение — установившееся.
Пренебрегая
скоростными
напорами
и 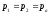
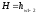 (126)
(126)
Потери напора 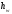 — вход в трубу, кран, два поворота, кран
и выход из трубы:
— вход в трубу, кран, два поворота, кран
и выход из трубы:
 (127)
(127)
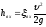 ;
; 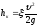
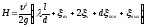 (128)
(128)
Обозначим 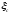 — коэффициент сопротивления системы.
— коэффициент сопротивления системы.
Так как 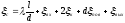 ,
,
то 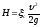 (129)
(129)
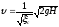 (130)
(130)
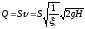 (131)
(131)
Обозначим: 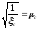 ,
,
тогда 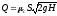 , (132)
, (132)
где 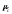 —
коэффициент расхода системы;
—
коэффициент расхода системы;
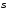 — площадь живого
сечения потока, м2.
— площадь живого
сечения потока, м2.
Второй случай:
Истечение жидкости в атмосферу (рис. 46).
Из уравнения Бернулли для сечений 1 — 1 и 2 — 2, получим
 (133)
(133)
где 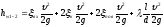 (134)
(134)
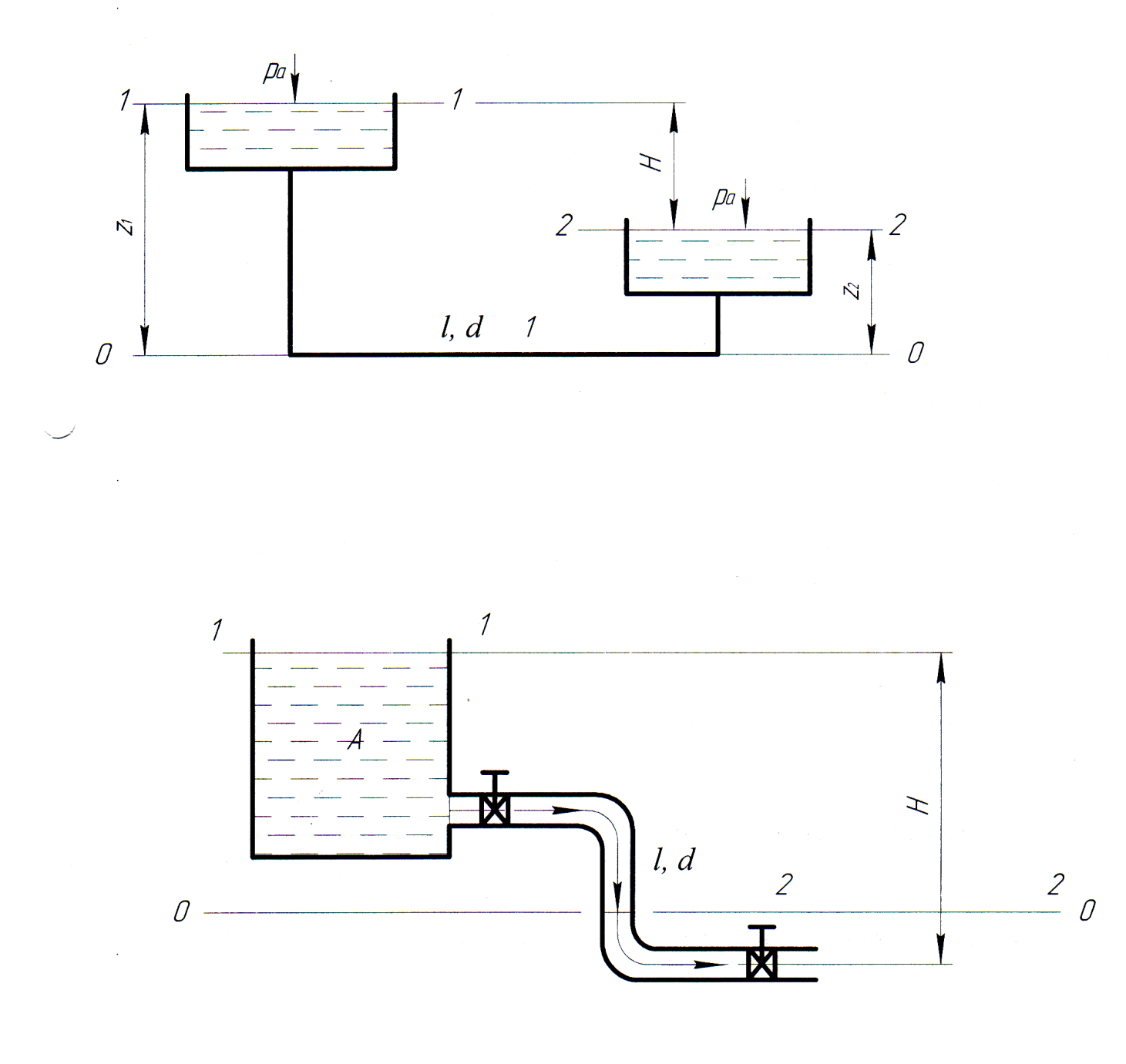
Рис. 46. Схема расчета короткого трубопровода (случай второй)
Подставив, имеем
 (135)
(135)
Обозначим 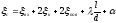 ,
,
тогда 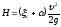 (136)
(136)
и 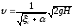 (137)
(137)
Расход жидкости: 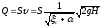 (138)
(138)
или 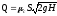 (139)
(139)
где 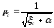 — коэффициент расхода системы.
— коэффициент расхода системы.
Пример. Определить
расход керосина Т-1
при температуре 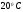 ,
протекающего по трубопроводу из сваренных
труб из нержавеющей стали в пункты 1
и 2 (рис. 47), если
напор Н в резервуаре постоянный и равный 7,2 м.
Длина отдельных частей трубопровода
,
протекающего по трубопроводу из сваренных
труб из нержавеющей стали в пункты 1
и 2 (рис. 47), если
напор Н в резервуаре постоянный и равный 7,2 м.
Длина отдельных частей трубопровода 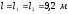 ,
диаметры:
,
диаметры: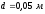 ,
,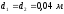 .
Местные потери напора в расчетах не
учитывать.
.
Местные потери напора в расчетах не
учитывать.
Решение: Так как трубы 1 и 2 параллельны, то потерянные напоры в этих трубах
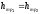
или 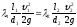 (140)
(140)
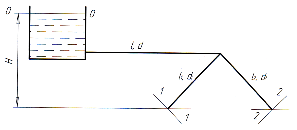
Рис. 47. Схема трубопровода с параллельными ветвями
По
условию задачи размеры параллельных
труб, изготовленных из одного материала,
одинаковы (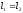 ,
,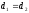 )
поэтому
)
поэтому
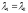 и
и 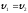
Следовательно,
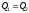 ;
;
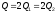 (141)
(141)
где 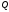 — расход
в трубопроводе;
— расход
в трубопроводе; 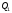 ,
,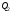 — расход в параллельных ветвях трубопровода.
— расход в параллельных ветвях трубопровода.
Уравнение Бернулли для сечений 0 — 0 и 1 — 1 (см. рис. 47)
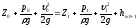
Так
как 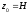 ,
,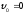 ,
, ,
,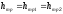 ,
,
то
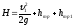
или
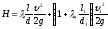 (142)
(142)
Уравнение
(142) можно решить только графоаналитическим
способом. Задаемся разными значениями
расхода жидкости в трубопроводе и для
этих значений 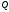 вычисляем
вычисляем  и
и 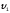 :
:
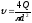 ;
;
(143)
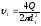 .
.
По
известным величинам  и
и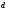 ,
,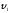 и
и 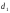 определяем
числа Рейнольдса
определяем
числа Рейнольдса 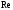 и
и 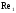 :
:
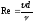 ,
, 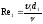 (144)
(144)
Для
керосина Т — 1 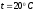 ,
,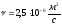 .
.
У
сварных труб из нержавеющей стали
эквивалентная шероховатость 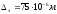 ,
поэтому относительная эквивалентная
шероховатость труб
,
поэтому относительная эквивалентная
шероховатость труб
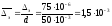 ;
;
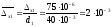 .
.
По
известным величинам 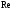 и
и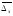 ,
,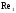 и
и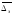 по графику Колбрука определяем
коэффициенты сопротивления трения
по графику Колбрука определяем
коэффициенты сопротивления трения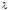 и
и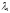 и далее по уравнению (142) устанавливаем
необходимый напор. Расчет сводим в табл.
5.
и далее по уравнению (142) устанавливаем
необходимый напор. Расчет сводим в табл.
5.
Таблица 5
Расчет гидравлической характеристики трубопроводов | |||
| 2 | 5 | 8 |
| 1,02 | 2,55 | 4,09 |
| 2,04 | 5,10 | 8,18 |
| 0,032 | 0,026 | 0,0245 |
| 0,053 | 0,332 | 0,851 |
| 0,312 | 1,54 | 3,83 |
| 0,795 | 1,99 | 3,19 |
| 1,27 | 3,18, | 5,10 |
| 0,032 | 0,0285 | 0,028 |
| 0,0322 | 0,202 | 0,519 |
| 0,23 | 1,33 | 3,34 |
| 0,574 | 3,07 | 7,69 |
Гидравлический расчет трубопроводов
Расчет коротких трубопроводов
Трубопровод называется коротким, если потери напора на местные сопротивления соизмеримы с потерями напора на трение. Поэтому при расчете учитываются и местные потери напора и потери напора на трение.
Трубопровод называется длинным, если потери напора на местные сопротивления гораздо меньше потерь напора на трение. В этом случае местные потери напора или не учитываются, или учитываются коэффициентом при потерях напора на трение:
Простым трубопроводомназывается трубопровод, состоящий из последовательно соединенных участков труб разного диаметра не имеющий боковых ответвлений.
При расчете трубопроводов встречаются три основных типа расчета, при известной длине трубопровода l, Свойств жидкости – плотностии динамическойили кинематической вязкости, геометрии трубопровода необходимо рассчитать:
давление pпо известным значениям диаметра трубопроводаDи расходeQ;
расход Qпо известным значениям диаметра трубопроводаDи давлениямp;
диаметра трубопровода Dпо известным значениям давленияpи расходеQ. Эта задача встречается при проектировании нового трубопровода или участка трубопровода.
Уравнение простого трубопровода
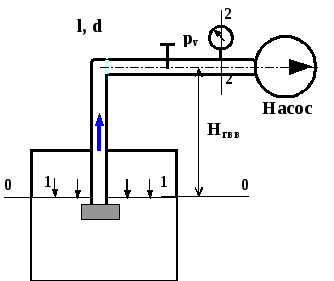
Рассмотрим вывод уравнения простого трубопровода для схемы короткого трубопровода показанного на рисунке 5.1. Насос из открытого бака перекачивает жидкость в сеть. На входе в насос стоит вакуумметр. Заданы свойства жидкости, материал трубопровода и геометрия трубопровода.
Рисунок 5.35 |
Для вывода уравнения простого трубопровода в данном случае:
1.5.1.1.Выберем два поперечных сечения там, где известны давления. Нумеруем эти сечения по направлению движения жидкости 1-1 и 2-2. Выбираем плоскость сравнения 0-0 проходящую через центр тяжести нижнего поперечного сечения.
1.5.1.2. Распишем значения z и p в этих поперечных сечениях. Для 5.1 z1= 0, z2= Hгвв, абсолютное давление в первом сечении равно атмосферному давлению p1= pат, абсолютное давление во втором сечении равно p2= pат— pv.
1.5.1.3. Распишем скорости в поперечных сечениях. Площадь первого поперечного сечения гораздо больше площади поперечного сечения трубы, поэтому скорость в первом поперечном сечении гораздо меньше скорости в трубе и примем её равной нулю v1= 0. Площадь второго поперечного сечения равна площади поперечного сечения трубы, поэтому скорость во втором поперечном сечении равна скорости в трубе v1= v. Подставим полученные значения в уравнении Бернулли для потока реальной жидкости:
| (5.0) |
Упрощая полученное уравнение, получим
| (5.0) |
1.5.1.4.Находим потери напора в трубопроводе. Потери напора равны сумме потерь напора на местные сопротивления и сумме потерь напора на трение. Местными потерями являются: потери напора на сетке с обратным клапаном, которая ставится на входе в трубу: поворот трубы на 90; задвижка на трубе. Все эти потери рассчитываются по скорости после местного сопротивления, а это скорость в трубе. По справочникам находим значения коэффициентов этих местных сопротивленийсетка,пов,зад. Потери напора на трение находится по формуле Дарси-Вейсбаха. Тогда потери напора равны
| (5.0) |
1.5.1.4.Подставим потери напора в уравнение Бернулли, получим:
| (5.0) |
Это и есть уравнение простого трубопровода для данного случая. Это уравнение не зависит от типа расчета трубопровода.
Расчет трубопроводов на прочность. Справочная книга
ПРЕДИСЛОВИЕОСНОВНЫЕ ПОЛОЖЕНИЯ РАСЧЕТА ПО ПРЕДЕЛЬНЫМ СОСТОЯНИЯМ
Основы расчета по предельным состояниям
Основные законы упруго-пластических деформаций
Ползучесть материалов
Колебания и усталость материалов
РАСЧЕТ ОТДЕЛЬНЫХ ЭЛЕМЕНТОВ ТРУБОПРОВОДОВ
Общпе положения
Расчет кривых труб на внутреннее давление
Расчет гибкости кривых труб
Расчет сварных из секторов кривых труб
Влияние внутреннего давления на гибкость кривых труб при изгибе
Напряжения в кривых трубах
Учет совместного воздействия внутреннего давления и изгиба
Расчет кривых труб на усталостную прочность
Расчет неусиленных тройников
Расчет усиленных тройников
Рекомендации по проектированию тройниковых соединений
Расчет конических переходов
Сферические заглушки
Линзовые компенсаторы
РАСЧЕТ ТРУБОПРОВОДОВ НА ТЕМПЕРАТУРНЫЕ ВОЗДЕЙСТВИЯ
Основные понятия
Методы расчета трубопроводов на температурные воздействия
Расчет простых трубопроводов методом сил
Определение единичных перемещений плоских простых трубопроводов
Определение температурных перемещений плоских простых трубопроводов
Решение системы канонических уравнений способом Гаусса
Определение усилий в элементах плоских простых трубопроводов
Типовые схемы расчета плоских простых трубопроводов
Расчет плоских простых трубопроводов способом «упругого центра»
Формулы для расчета плоских простых трубопроводов различной конфигурации на температурные воздействия
Расчет плоских простых трубопроводов с шарнирами
Графики для определения вылета и упругого отпора П-образных компенсаторов
Приближенный способ расчета пространственных простых трубопроводов
на температурные воздействия
РАСЧЕТ ТРУБОПРОВОДОВ, УКЛАДЫВАЕМЫХ НА ОПОРЫ
Определение толщины стенки трубы
Определение допускаемого пролета трубопроводов
Определение нагрузок, действующих на опоры трубопроводов
РАСЧЕТ ПОДЗЕМНЫХ МАГИСТРАЛЬНЫХ ТРУБОПРОВОДОВ
Основные положения
Силовые воздействия, влияющие на работу трубопроводов
Требования к трубам для магистральных трубопроводов
Определение толщины стенок труб магистральных трубопроводов
Минимально допустимая толщина стенок труб
Глубина заложения магистральных трубопроводов
Расчет анкерных креплений трубопроводов
Определение толщины стенок защитных кожухов для пропуска трубопроводов под железнодорожными насыпями
Расчет асбестоцементных труб
РАСЧЕТ НАДЗЕМНЫХ МАГИСТРАЛЬНЫХ ТРУБОПРОВОДОВ
Общие положения
Основы расчета
Расчет балочных и консольных переходов
Расчет надземных трубопроводов при прокладке их «змейкой»
Расчет компенсаторов при надземной прокладке трубопроводов
Определение нагрузок , действующих на опоры надземных магистральных
трубопроводов
РАСЧЕТ ПОДЗЕМНЫХ ТРУБОПРОВОДОВ, УКЛАДЫВАЕМЫХ В РАЙОНАХ ГОРНЫХ РАЗРАБОТОК
Основные положения
Характер деформаций земной поверхности в районах горных разработок
и их влияние на работу трубопроводов
Величина деформаций земной поверхности
Продолжительность процесса сдвижения земной поверхности
Безопасная глубина подработки
Определение деформаций земной поверхности применительно к
расчету трубопроводов
Расчет трубопроводов
Конструктивные мероприятия по защите трубопроводов от вредного
влияния горных разработок
РАСЧЕТ ТРУБОПРОВОДОВ НА КОЛЕБАНИЯ
Собственные частоты колебаний трубопроводов, лежащих на жестких опорах
Собственные частоты колебаний трубопроводов, имеющих упругие опоры
Собственная частота колебаний Л-образного компенсатора
Собственные частоты колебаний арочных трубопроводов
Колебания висячих трубопроводов
Динамическое действие ветровой нагрузки на трубопроводы
Мероприятия по уменьшению колебаний
Расчет трубопроводов на сейсмические воздействия
Приложения
Приложение I. Геометрические характеристики и вес труб
Приложение II. Значения модулей упругости и коэффициентов линейного расширения трубных сталей
Приложение III. Механические характеристики металла труб в состоянии поставки
Литература

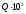 ,
, 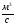
 ,
, 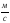
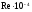
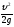 ,
,
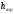 ,
, 
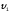 ,
, 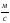
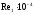
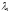
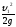 ,
,
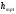 ,
, 
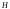 ,
,
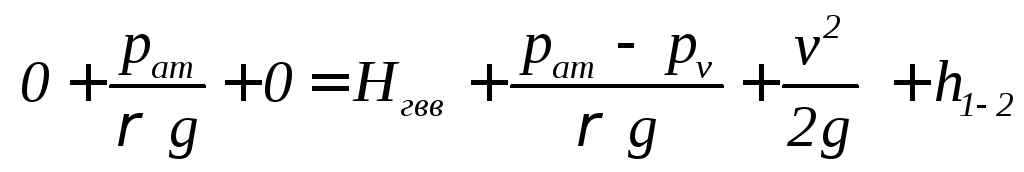 .
.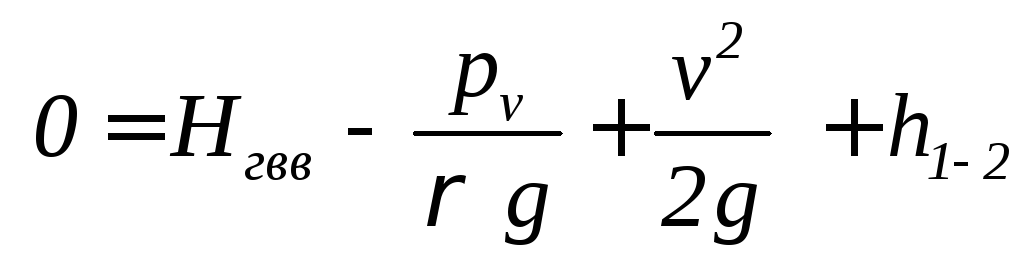 .
.